Strength of Materials PYQ Set (2000 to 2025)

📝 In the engineering stress-strain curve for mild steel, the Ultimate Tensile Strength (UTS) refers to ____ .

(A) Yield stress
(B) Proportional limit
(C) Maximum stress
(D) Fracture stress

Solution =

The Ultimate Tensile Strength (UTS) refers to the maximum stress a material can withstand before necking begins. It is the highest point on the engineering stress-strain curve.

Correct answer: (C) Maximum stress

📝 The spring constant of a helical compression spring DOES NOT depend on:

(A) Coil diameter
(B) Material strength
(C) Number of active turns
(D) Wire diameter

Solution =

⦾ Spring Constant Formula:
The spring constant $ k $ of a helical compression spring is given by:
\[ k = \frac{G d^4}{8 D^3 N} \] where:
✓ $ G $ = Shear modulus of the material (stiffness property, not strength)
✓ $ d $ = Wire diameter
✓ $ D $ = Coil diameter
✓ $ N $ = Number of active turns

⦾ Dependencies:
✓ Coil diameter (D): Directly appears in the formula ($ k \propto \frac{1}{D^3} $).
✓ Material strength: The formula uses shear modulus $ G $ (a stiffness property), not material strength (e.g., yield strength or tensile strength). Strength affects load capacity but not spring constant.
✓ Number of active turns (N): Directly appears in the formula ($ k \propto \frac{1}{N} $).
✓ Wire diameter (d): Directly appears in the formula ($ k \propto d^4 $).

⦾ Key Insight:
The spring constant depends on geometry (d, D, N) and material stiffness (G), but not on material strength (e.g., yield strength or ultimate strength).

⦾ The correct option is: b) material strength

📝 An axial residual compressive stress due to a manufacturing process is present on the outer surface of a rotating shaft subjected to bending. Under a given bending load, the fatigue life of the shaft in the presence of the residual compressive stress is ____ .

(A) Decreased
(B) Increased or decreased, depending on the external bending load
(C) Neither decreased nor increased
(D) Increased

Solution =

The correct answer is: d) increased

Explanation:
Residual compressive stress on the outer surface of a rotating shaft helps counteract the tensile stresses induced by bending.
Since fatigue failure typically initiates at surface cracks under tensile stress, compressive residual stress reduces the effective tensile stress and thereby
delays crack initiation.

As a result, the fatigue life of the shaft increases.
So, the presence of axial residual compressive stress increases the fatigue life under a given bending load.

📝 A simply supported laterally loaded beam was found to deflect more than a specified value. Which of the following measures will reduce the deflection?

(A) Increase the area moment of inertia
(B) Increase the span of the beam
(C) Select a different material having lesser modulus of elasticity
(D) Magnitude of the load to be increased

Solution =

Step 1: Understand Deflection Formula
For a simply supported beam with central point load, maximum deflection ($ \delta_{max} $) is:
\[ \delta_{max} = \frac{PL^3}{48EI} \]
Where:
$ P $ = Load magnitude
$ L $ = Span length
$ E $ = Modulus of elasticity
$ I $ = Area moment of inertia
Deflection is inversely proportional to $ EI $ (flexural rigidity).

Step 2: Analyze Each Option

Option a) Increase the area moment of inertia
Since $ \delta \propto \frac{1}{I} $, increasing $ I $ will reduce deflection.
This can be achieved by:
✓ Using deeper beam sections
✓ Adding flanges (I-beams)
✓ Changing cross-section shape
This is a correct measure.

Option b) Increase the span of the beam
Since $ \delta \propto L^3 $, increasing span would dramatically increase deflection.
This would worsen the problem.

Option c) Select material with lesser modulus of elasticity
Since $ \delta \propto \frac{1}{E} $, reducing $ E $ would increase deflection.
This is opposite of what we want.

Option d) Increase the load magnitude
Since $ \delta \propto P $, increasing load would increase deflection linearly.
This would worsen the deflection.

Step 3: Summary of Effective Measures
To reduce deflection, we can:
Increase moment of inertia (most effective structural change)
Use material with higher modulus of elasticity
Reduce beam span (if possible)
Decrease applied load
Add additional supports (changes boundary conditions)

Final Answer: The only correct option among the given choices is: \[ \boxed{a} \]

📝 A rod of length L and diameter D is subjected to a tensile load P. Which of the following is sufficient to calculate the resulting change in diameter?

(A) Young’s modulus
(B) Shear modulus
(C) Poisson’s ratio
(D) Both Young’s modulus and shear modulus

Solution =

To determine the change in diameter of the rod under a tensile load, we need to consider the lateral strain caused by the axial strain. This relationship is governed by Poisson’s ratio ($\nu$). Here’s the step-by-step explanation:

Key Concepts:
⦾ Axial Strain ($\epsilon_{\text{axial}}$): When a tensile load $P$ is applied, the rod elongates, and the axial strain is given by: \[ \epsilon_{\text{axial}} = \frac{\sigma}{E} \] where: $\sigma = \frac{P}{A}$ is the axial stress ($A$ is the cross-sectional area),
$E$ is Young’s modulus.
⦾ Lateral Strain ($\epsilon_{\text{lateral}}$): Due to Poisson’s effect, the rod’s diameter changes. The lateral strain is related to the axial strain by Poisson’s ratio ($\nu$): \[ \epsilon_{\text{lateral}} = -\nu \cdot \epsilon_{\text{axial}} \] The negative sign indicates that the diameter decreases under tensile load.
⦾ Change in Diameter ($\Delta D$): The change in diameter is calculated using the lateral strain: \[ \Delta D = \epsilon_{\text{lateral}} \cdot D \] Substituting the expression for lateral strain: \[ \Delta D = -\nu \cdot \epsilon_{\text{axial}} \cdot D \]
Required Parameters:
To calculate the change in diameter ($\Delta D$), we need:
➤ Poisson’s ratio ($\nu$): Relates lateral strain to axial strain.
➤ Axial strain ($\epsilon_{\text{axial}}$): Depends on Young’s modulus ($E$) and the applied stress ($\sigma$).
Thus, both Young’s modulus and Poisson’s ratio are required to calculate the change in diameter.

Why Other Options Are Incorrect:
➤ Shear modulus ($G$): Shear modulus relates to shear stress and shear strain, which are not directly relevant to the change in diameter under axial loading.
➤ Young’s modulus alone: While Young’s modulus is needed to calculate axial strain, it is insufficient without Poisson’s ratio to determine lateral strain.
➤ Poisson’s ratio alone: Poisson’s ratio alone cannot determine the change in diameter without knowing the axial strain (which depends on Young’s modulus).

Final Answer: d) Both Young’s modulus and Poisson’s ratio

📝 The transverse shear stress acting in a beam of rectangular cross-section, subjected to a transverse shear load, is _____ .

(A) Variable with maximum at the bottom of the beam
(B) Variable with maximum at the top of the beam
(C) Uniform
(D) Variable with maximum on the neutral axis

Solution =

The transverse shear stress $ \tau $ in a beam of rectangular cross-section subjected to a transverse shear force is given by:
\[ \tau = \frac{VQ}{Ib} \]
Where:
✓ $ V $ = Shear force on the cross-section
✓ $ Q $ = First moment of area about the neutral axis
✓ $ I $ = Moment of inertia of the entire cross-section
✓ $ b $ = Width of the section at the point where shear is being calculated

This shear stress distribution is parabolic:
✓ Maximum at the neutral axis (middle height of the beam)
✓ Zero at the top and bottom surfaces of the beam

Correct Answer: d) Variable with maximum on the neutral axis

📝 Two identical cantilever beams are supported as shown, with their free ends in contact through a rigid roller. After the load P is applied, the free ends will have

(A) Equal deflections but not equal slopes
(B) Equal slopes but not equal deflections
(C) Equal slopes as well as equal deflections
(D) Neither equal slopes nor equal deflections

Solution =

Two identical cantilever beams are supported such that their free ends are in contact via a rigid roller. A vertical load $ P $ is applied at the point of contact.

Key Observations:
⦾ The rigid roller enforces equal vertical deflections at the point of contact.
⦾ The roller does not resist rotation, so the beams can have different slopes at that point.
⦾ Even though the beams are identical, this interaction affects slope but not deflection.

Correct Answer: Equal deflections but not equal slopes

\[ \text{Deflections: } \delta_1 = \delta_2 \quad \] \[\text{(due to rigid roller)} \] \[ \text{Slopes: } \theta_1 \ne \theta_2 \quad \] \[\text{(rotation is free at roller)} \]

📝 Two identical circular rods of same diameter and same length are subjected to same magnitude of axial tensile force. One of the rod is made out of mild steel having the modulus of elasticity of 206 GPa. The other rod is made out of cast iron having the modulus of elasticity of 100 GPa. Assume both the materials to be homogeneous and isotropic and the axial force causes the same amount of uniform stress in both the rods. The stresses developed are within the proportional limit of the respective materials. Which of the following observations is correct?

(A) Both rods elongate by the same amount
(B) Mild steel rod elongates more than the cast iron rod
(C) Cast iron rod elongates more than the mild steel rods
(D) As the stresses are equal strains are also equal in both the rods

Solution =

Given:
✓ Two identical circular rods: Same diameter ($d$)
Same length ($L$)
Both are subjected to the same axial tensile force ($F$).
✓ Materials: Mild steel: Modulus of elasticity ($E_{\text{steel}} = 206 \, \text{GPa}$)
✓ Cast iron: Modulus of elasticity ($E_{\text{iron}} = 100 \, \text{GPa}$)
✓ Both rods experience the same uniform stress ($\sigma$).
✓ The stresses are within the proportional limit of the respective materials.

Key Concepts:
⦾ Stress ($\sigma$): Defined as force per unit area. Since the rods have the same diameter and are subjected to the same force, the stress in both rods is the same. \[ \sigma = \frac{F}{A} \] where $A$ is the cross-sectional area of the rod.
⦾ Strain ($\epsilon$): Defined as the ratio of elongation ($\Delta L$) to the original length ($L$). \[ \epsilon = \frac{\Delta L}{L} \]
⦾ Hooke’s Law: Relates stress and strain through the modulus of elasticity ($E$): \[ \sigma = E \cdot \epsilon \] Rearranging for strain: \[ \epsilon = \frac{\sigma}{E} \]
Analysis:
Since the stress ($\sigma$) is the same in both rods, the strain ($\epsilon$) in each rod depends on the modulus of elasticity ($E$): \[ \epsilon_{\text{steel}} = \frac{\sigma}{E_{\text{steel}}} \] \[ \epsilon_{\text{iron}} = \frac{\sigma}{E_{\text{iron}}} \]
Given that $E_{\text{steel}} > E_{\text{iron}}$, it follows that: \[ \epsilon_{\text{steel}} < \epsilon_{\text{iron}} \]
This means the cast iron rod will experience more strain (elongation) than the mild steel rod.

The correct observation is: c) Cast iron rod elongates more than the mild steel rod

📝 The beams, one having square cross section and another circular cross-section, are subjected to the same amount of bending moment. If the cross sectional area as well as the material of both the beams are same then

(A) Maximum bending stress developed in both beams is same
(B) Circular beam experiences more bending stress than square one
(C) Square beam experiences more bending stress than circular one
(D) As material is same, both beams will experience same deformation

Solution =

Step 1: Understand Bending Stress Formula
The maximum bending stress ($ \sigma_{max} $) is given by:
\[ \sigma_{max} = \frac{M \cdot y}{I} \] Where:
✓ $ M $ = Bending moment (same for both beams)
✓ $ y $ = Distance from neutral axis to extreme fiber
✓ $ I $ = Moment of inertia of cross-section

The section modulus ($ Z = \frac{I}{y} $) determines resistance to bending:
\[ \sigma_{max} = \frac{M}{Z} \] Lower section modulus means higher bending stress for same moment.

Step 2: Calculate Properties for Both Cross-Sections
Let cross-sectional area = $ A $ (same for both)
⦾ Square Cross-Section
Side length ($ a $):
\[ a = \sqrt{A} \] Section modulus: \[ Z_{square} = \frac{a^3}{6} = \frac{A^{3/2}}{6} \]
⦾ Circular Cross-Section
Diameter ($ d $):
\[ A = \frac{\pi d^2}{4} \implies d = \sqrt{\frac{4A}{\pi}} \] Section modulus: \[ Z_{circle} = \frac{\pi d^3}{32} = \frac{\pi}{32}\left(\frac{4A}{\pi}\right)^{3/2} = \frac{A^{3/2}}{8\sqrt{\pi}} \]
Step 3: Compare Section Moduli
Calculate ratio of section moduli:
\[ \frac{Z_{circle}}{Z_{square}} = \frac{\frac{A^{3/2}}{8\sqrt{\pi}}}{\frac{A^{3/2}}{6}} = \frac{6}{8\sqrt{\pi}} \approx 0.423 \] This shows:
\[ Z_{circle} \approx 0.423 \times Z_{square} \] Thus, the circular section has lower section modulus than the square section for the same area.

Step 4: Determine Bending Stress
Since $ \sigma_{max} = \frac{M}{Z} $ and $ M $ is same:
✓ Lower $ Z $ ⇒ Higher $ \sigma_{max} $
✓ Circular beam has lower $ Z $ ⇒ Higher bending stress

Therefore, the circular beam experiences more bending stress than the square beam.
Final Answer: b Circular beam has more stress

📝 If σ1 and σ3 are the algebraically largest and smallest principal stresses, respectively, the value of the maximum shear stress is ____ .

(A) $\frac{\sigma_1 + \sigma_3}{2}$
(B) $\frac{\sigma_1 – \sigma_3}{2}$
(C) $\sqrt{\frac{\sigma_1 + \sigma_3}{2}}$
(D) $\sqrt{\frac{\sigma_1 – \sigma_3}{2}}$

Solution =

To determine the maximum shear stress given the principal stresses $\sigma_1$ (algebraically largest) and $\sigma_3$ (algebraically smallest), we use the following formula:
\[ \tau_{\text{max}} = \frac{\sigma_1 – \sigma_3}{2} \]
Explanation:
⦾ The maximum shear stress occurs on a plane oriented at 45° to the principal stress directions.
⦾ It is calculated as half the difference between the largest and smallest principal stresses.

📝 The second moment of a circular area about the diameter is given by (D is the diameter).

(A) $ \frac{\pi D^4}{4} $
(B) $ \frac{\pi D^4}{16} $
(C) $ \frac{\pi D^4}{32} $
(D) $ \frac{\pi D^4}{64} $

Understanding the Second Moment of Area (Moment of Inertia):
The second moment of area, also known as the moment of inertia, measures an object’s resistance to bending. For a circular area, the moment of inertia about its diameter is a standard formula.

Given Parameters:
✓ Diameter of the circle: $ D $
✓ Radius of the circle: $ r = \frac{D}{2} $

Standard Formula: The moment of inertia of a circle about its diameter is:
\[ I = \frac{\pi r^4}{4} \] Substituting $ r = \frac{D}{2} $:
\[ I = \frac{\pi \left(\frac{D}{2}\right)^4}{4} = \frac{\pi D^4}{64} \] The correct match is option d.
Final Answer: \[ \boxed{d} \]

📝 A concentrated load of P acts on a simply supported beam of span L at a distance L/3 from the left support. The bending moment at the point of application of the load is given by

(A) $ \frac{PL}{3} $
(B) $ \frac{2PL}{3} $
(C) $ \frac{PL}{9} $
(D) $ \frac{2PL}{9} $

Solution =

Step 1: Understand the Problem A simply supported beam of length $ L $ carries a concentrated load $ P $ at $ \frac{L}{3} $ from the left support. We need to find the bending moment at this point.

Step 2: Calculate Support Reactions
Let $ R_A $ and $ R_B $ be the reactions at left and right supports respectively.
Taking moments about support B:
\[ \sum M_B = 0 \implies \]\[ R_A \cdot L – P \cdot \left(L – \frac{L}{3}\right) = 0 \] \[ R_A \cdot L = P \cdot \frac{2L}{3} \implies R_A = \frac{2P}{3} \] Sum of vertical forces: \[ R_A + R_B = P \implies \]\[\frac{2P}{3} + R_B = P \implies R_B = \frac{P}{3} \]
Step 3: Calculate Bending Moment
The bending moment at $ \frac{L}{3} $ from left support:
\[ M = R_A \cdot \frac{L}{3} = \frac{2P}{3} \cdot \frac{L}{3} = \frac{2PL}{9} \] Alternatively, using $ R_B $:
\[ M = R_B \cdot \left(L – \frac{L}{3}\right) = \frac{P}{3} \cdot \frac{2L}{3} \]\[= \frac{2PL}{9} \] Both methods give the same result.

Step 4: Match with Options
The bending moment is $ \frac{2PL}{9} $, which corresponds to option d.
Final Answer: \[ \boxed{d} \]

📝 If the principal stresses in a plane stress problem are σ1 = 100 MPa, σ2 = 40 MPa, the magnitude of the maximum shear stress (in MPa) will be ____ .

(A) 60
(B) 50
(C) 30
(D) 20

Solution =

To solve this problem, we need to determine the maximum shear stress in a plane stress problem given the principal stresses $\sigma_1$ and $\sigma_2$. Here’s the step-by-step solution:

Key Concepts:
Principal Stresses: In a plane stress problem, the principal stresses $\sigma_1$ and $\sigma_2$ are the normal stresses acting on planes where the shear stress is zero.

Maximum Shear Stress: The maximum shear stress ($\tau_{\text{max}}$) in a plane stress problem is given by: \[ \tau_{\text{max}} = \frac{|\sigma_1 – \sigma_2|}{2} \] This formula calculates the maximum shear stress as half the difference between the two principal stresses.

Given:
Principal stresses: \[ \sigma_1 = 100 \, \text{MPa}, \quad \sigma_2 = 40 \, \text{MPa} \]

Calculation:
Using the formula for maximum shear stress: \[ \tau_{\text{max}} = \frac{|\sigma_1 – \sigma_2|}{2} \] Substitute the given values: \[ \tau_{\text{max}} = \frac{|100 – 40|}{2} = \frac{60}{2} = 30 \, \text{MPa} \]

Final Answer: c) 30

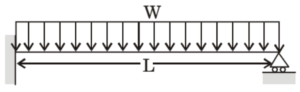
📝 A beam of length L is carrying a uniformly distributed load w per unit length. The flexural rigidity of the beam is EI. The reaction at the simple support at the right end is

(A) $ \frac{wL}{2} $
(B) $ \frac{3wL}{8} $
(C) $ \frac{wL}{4} $
(D) $ \frac{wL}{8} $

Solution =

This is a case of a propped cantilever beam subjected to a uniformly distributed load $ w $ over the entire span $ L $.
To find the reaction at the right end (simple support), we use the standard result:
\[ R_B = \frac{3wL}{8} \]
Hence, the correct answer is: $ \boxed{ \frac{3wL}{8} } $

📝 A two-dimensional fluid element rotates like a rigid body. At a point within the element, the pressure is 1 unit. Radius of Mohr’s circle, characterizing the state of stress at that point, is ____ .

(A) 2 unit
(B) 0.5 unit
(C) 0 unit
(D) 1 unit

Solution =

Given: A two-dimensional fluid element rotates like a rigid body.
Pressure at a point is 1 unit.

Key Concept: Fluids cannot sustain shear stress at rest or in rigid body rotation. So:
Normal stresses: $ \sigma_x = \sigma_y = -p = -1 \, \text{unit} $
Shear stress: $ \tau_{xy} = 0 $

Radius of Mohr’s Circle:
$ R = \sqrt{ \left( \frac{\sigma_x – \sigma_y}{2} \right)^2 + \tau_{xy}^2 } $

Substituting the values:
$ R = \sqrt{ \left( \frac{-1 – (-1)}{2} \right)^2 + 0^2 } = \sqrt{0} = 0 $

Final Answer: C. 0 unit

📝 The state of stress at a point under plane stress condition is: $ \sigma_{xx} = 40 \, \text{MPa} $
$ \sigma_{yy} = 100 \, \text{MPa} $
$ \tau_{xy} = 40 \, \text{MPa} $
The radius of the Mohr’s circle representing the given state of stress in MPa is ____ .

(A) 40
(B) 50
(C) 60
(D) 100

Solution =

Given:
$ \sigma_{xx} = 40 \, \text{MPa} $
$ \sigma_{yy} = 100 \, \text{MPa} $
$ \tau_{xy} = 40 \, \text{MPa} $

Formula:
$ R = \sqrt{ \left( \frac{\sigma_{xx} – \sigma_{yy}}{2} \right)^2 + \tau_{xy}^2 } $

Substitute values:
$ R = \sqrt{ \left( \frac{40 – 100}{2} \right)^2 + (40)^2 } $$= \sqrt{(-30)^2 + 1600} = \sqrt{2500} $$= 50 \, \text{MPa} $

Final Answer: b) 50 MPa

📝 A rod of length L having uniform cross-sectional area A is subjected to a tensile force P as shown in the figure below. If the Young’s modulus of the material varies linearly from E1 to E2 along the length of the rod, the normal stress developed at the section-S is

(A) $\frac{P}{A}$
(B) $\frac{P(E_1 – E_2)}{A(E_1 + E_2)}$
(C) $\frac{PE_2}{AE_1}$
(D) $\frac{PE_1}{PE_2}$

Solution =

To determine the normal stress developed at section $ S $ of the rod, we need to consider the variation in Young’s modulus along the length of the rod. Here’s the step-by-step solution:

Given:
⦾ A rod of length $ L $ with a uniform cross-sectional area $ A $.
⦾ A tensile force $ P $ is applied.
⦾ Young’s modulus varies linearly from $ E_1 $ at one end to $ E_2 $ at the other end.

Key Concepts:
✓ Normal Stress ($\sigma$): Normal stress is defined as the force per unit area: \[ \sigma = \frac{P}{A} \]
✓ Young’s Modulus Variation: Since Young’s modulus varies linearly along the length of the rod, the stress distribution will also be influenced by this variation.

Analysis:
At any section $ S $ of the rod, the normal stress can be calculated using the formula: \[ \sigma = \frac{P}{A} \] This formula is valid regardless of the variation in Young’s modulus along the length of the rod, as long as the cross-sectional area $ A $ is uniform.

Conclusion:
The normal stress developed at section $ S $ is: \[ \sigma = \frac{P}{A} \]
Final Answer: a) $\frac{P}{A}$

📝 In terms of Poisson’s ratio (υ) the ratio of Young’s Modulus (E) to Shear Modulus (G) of elastic materials is

(A) 2 (1 + υ)
(B) 2 (1 − υ)
(C) 1/2 (1 + υ)
(D) 1 /2 (1 − υ)

Solution =

To solve this problem, we need to find the relationship between Young’s Modulus ($E$), Shear Modulus ($G$), and Poisson’s Ratio ($\nu$) for elastic materials. Here’s the step-by-step solution:

Key Concepts:
⦾ Young’s Modulus ($E$): Young’s modulus measures the stiffness of a material and is defined as the ratio of stress to strain in the axial direction.
⦾ Shear Modulus ($G$): Shear modulus measures the material’s resistance to shear deformation and is defined as the ratio of shear stress to shear strain.
⦾ Poisson’s Ratio ($\nu$): Poisson’s ratio is the ratio of transverse strain to axial strain when a material is subjected to axial stress.
⦾ Relationship Between $E$, $G$, and $\nu$: For isotropic elastic materials, the relationship between Young’s modulus ($E$), shear modulus ($G$), and Poisson’s ratio ($\nu$) is given by: \[ E = 2G(1 + \nu) \] Rearranging this equation, we can express the ratio of $E$ to $G$ as: \[ \frac{E}{G} = 2(1 + \nu) \]
Calculation:
From the relationship: \[ E = 2G(1 + \nu) \] Divide both sides by $G$: \[ \frac{E}{G} = 2(1 + \nu) \]
The ratio of Young’s Modulus ($E$) to Shear Modulus ($G$) in terms of Poisson’s ratio ($\nu$) is: \[ \frac{E}{G} = 2(1 + \nu) \]
Final Answer: a) $2(1 + \nu)$

📝 The Poisson’s ratio for a perfectly incompressible linear elastic material is ____ .

(A) 1
(B) 0.5
(C) 0
(D) Infinity

Solution =

Concept:
Poisson’s ratio ($\nu$) is defined as the negative ratio of transverse strain to axial strain:
\[ \nu = -\frac{\varepsilon_{\text{transverse}}}{\varepsilon_{\text{axial}}} \]
For a perfectly incompressible material (volume remains constant during deformation):

Derivation:
For a material under uniaxial stress, the volume change $\Delta V/V$ is given by:
\[ \frac{\Delta V}{V} = \varepsilon_{\text{axial}} + 2\varepsilon_{\text{transverse}} \]
For incompressibility ($\Delta V = 0$):
\[ \varepsilon_{\text{axial}} + 2\varepsilon_{\text{transverse}} = 0 \]
\[ \Rightarrow \varepsilon_{\text{transverse}} = -\frac{1}{2}\varepsilon_{\text{axial}} \]
Substituting into Poisson’s ratio definition:
\[ \nu = -\left(-\frac{1}{2}\right) = 0.5 \]
Evaluating the Options:

(A) 1 = Would imply no transverse deformation (violates incompressibility)
(B) 0.5 = Correct value for incompressible materials
(C) 0 = Would imply no transverse strain (not incompressible)
(D) Infinity = Physically impossible for stable materials

Final Answer:
\[ \boxed{B} \]

📝 An initially stress-free massless elastic beam of length L and circular cross-section with diameter d. (d<<L) is held fixed between two walls as shown. The beam material has Young’s modulus E and coefficient of thermal expansion α . If the beam is slowly and uniformly heated, the temperature rise required to cause the beam to buckle is proportional to _____ .

(A) $ d $
(B) $ d^2 $
(C) $ d^3 $
(D) $ d^4 $

Solution =

For a beam fixed at both ends, thermal expansion creates compressive stress, which can lead to buckling when the axial compressive force exceeds a critical value.

Step 1: Expression for Critical Buckling Load
The critical buckling load $ P_{cr} $ for a beam of length $ L $ with a circular cross-section of diameter $ d $ is given by Euler’s formula:
\[ P_{cr} = \frac{\pi^2 EI}{L^2} \]
where $ E $ is Young’s modulus, and $ I $ is the area moment of inertia for a circular cross-section:
\[ I = \frac{\pi d^4}{64} \]
Substituting $ I $ into the buckling formula:
\[ P_{cr} = \frac{\pi^3 E d^4}{64 L^2} \]
Step 2: Thermal Force due to Expansion
The thermal stress $ \sigma $ induced by a temperature rise $ \Delta T $ in a fully restrained beam is:
\[ \sigma = E \alpha \Delta T \]
The total compressive force due to thermal expansion is:
\[ P_{thermal} = A \sigma = \left(\frac{\pi d^2}{4}\right) E \alpha \Delta T \]
Step 3: Equating Thermal Force to Buckling Load
At the onset of buckling, we equate:
\[ P_{thermal} = P_{cr} \]
\[ \left(\frac{\pi d^2}{4}\right) E \alpha \Delta T = \frac{\pi^3 E d^4}{64 L^2} \]
Canceling $ E $ and solving for $ \Delta T $:
\[ \Delta T = \frac{\pi^2 d^2}{16 L^2 \alpha} \]
Step 4: Proportionality Relation
Thus, the required temperature rise for buckling is:
\[ \Delta T \propto d^2 \]
Final Answer: (B) $ d^2 $

📝 A cantilever beam of length L is subjected to a moment M at the free end. The moment of inertia of the beam cross section about the neutral axis is I and the Young’s modulus is E The magnitude of the maximum deflection is ?

(A) $\frac{ML^2}{2EI}$
(B) $\frac{ML^2}{EI}$
(C) $\frac{2ML^2}{EI}$
(D) $\frac{4ML^2}{EI}$

Solution =

For a cantilever beam with a moment $ M $ applied at the free end, the maximum deflection $ \delta_{\text{max}} $ occurs at the free end and is given by:
\[ \delta_{\text{max}} = \frac{ML^2}{2EI} \]
Explanation:
⦾ The deflection of a cantilever beam under a moment at the free end is derived from the Euler-Bernoulli beam theory.
⦾ The curvature of the beam is proportional to the applied moment, and integrating this curvature twice gives the deflection.
⦾ The factor $ \frac{1}{2} $ comes from the integration process and the boundary conditions (fixed at one end, free at the other).

Correct Answer:
\[ \frac{ML^2}{2EI} \]

📝 A solid circular shaft of 60 mm diameter transmits a torque of 1600 Nm. The value of maximum shear stress developed is:

(A) 37.72 MPa
(B) 47.72 MPa
(C) 57.72 MPa
(D) 67.72 MPa

Solution =

The maximum shear stress $ \tau_{\text{max}} $ in a solid circular shaft under torsion is given by:
\[ \tau_{\text{max}} = \frac{16T}{\pi d^3} \] where:
$ T = 1600 $ Nm is the applied torque,
$ d = 60 $ mm $ = 60 \times 10^{-3} $ m is the diameter of the shaft.

Substituting the values:
\[ \tau_{\text{max}} = \frac{16 \times 1600}{\pi \times (60 \times 10^{-3})^3} \] \[ \tau_{\text{max}} = \frac{25600}{\pi \times 2.16 \times 10^{-4}} \] \[ \tau_{\text{max}} = \frac{25600}{3.1416 \times 2.16 \times 10^{-4}} \] \[ \tau_{\text{max}} \approx 37.72 \times 10^6 \text{ Pa} = 37.72 \text{ MPa} \] Explanation:
➤ The formula for maximum shear stress in a circular shaft is derived from torsion theory.
➤ The stress is directly proportional to the applied torque and inversely proportional to the cube of the shaft diameter.
➤ Unit consistency is crucial (diameter converted to meters).

The correct option is: a) 37.72 MPa

📝 In a plane stress condition, the components of stress at a point are
$ \sigma_x = 20 \, \text{MPa} $
$ \sigma_y = 80 \, \text{MPa} $
$ \tau_{xy} = 40 \, \text{MPa} $
The maximum shear stress (in MPa) at the point is ____.

(A) 20
(B) 25
(C) 50
(D) 100

Solution =

Formula for Maximum Shear Stress:
$ \tau_{\text{max}} = \sqrt{ \left( \frac{\sigma_x – \sigma_y}{2} \right)^2 + \tau_{xy}^2 } $

Substituting values:
$ \tau_{\text{max}} = \sqrt{ \left( \frac{20 – 80}{2} \right)^2 + 40^2 } $$= \sqrt{(-30)^2 + 1600} = \sqrt{2500} $$= 50 \, \text{MPa} $

Correct Answer: c) 50 MPa

📝 A pin-ended column of length L, modulus of elasticity E, and second moment of the cross-sectional area I is loaded concentrically by a compressive load P. The critical buckling load (Pcr) is given by

(A) $ P_{cr} = \frac{EI}{\pi^2 L^2} $
(B) $ P_{cr} = \frac{\pi^2 EI}{3L^2} $
(C) $ P_{cr} = \frac{\pi EI}{L^2} $
(D) $ P_{cr} = \frac{\pi^2 EI}{L^2} $

Solution =

The critical buckling load of a long, slender column under axial compressive force is given by Euler’s formula:
$ P_{\text{cr}} = \frac{\pi^2 E I}{(K L)^2} $

Where:
$ E $ is the modulus of elasticity
$ I $ is the second moment of area of the column cross-section
$ L $ is the length of the column
$ K $ is the effective length factor

For a pin-ended column (both ends hinged), $ K = 1 $, so the formula simplifies to:
$ P_{\text{cr}} = \frac{\pi^2 E I}{L^2} $

Correct Answer: Option (d)

📝 A shaft subjected to torsion experiences pure shear stress τ on the surface. The maximum principal stress on the surface which is at 45° to the axis will have a value

(A) τ cos 45°
(B) 2τ cos 45°
(C) τ cos² 45°
(D) 2τ sin 45° cos 45°

Solution =

To solve this problem, we need to determine the maximum principal stress on the surface of a shaft subjected to torsion, where the surface experiences pure shear stress $\tau$. The maximum principal stress occurs at an angle of $45^\circ$ to the axis of the shaft.

Key Concepts:
⦾ Pure Shear Stress: In a shaft subjected to torsion, the surface experiences pure shear stress $\tau$. This shear stress acts tangentially to the surface.
⦾ Principal Stresses: Principal stresses are the normal stresses that occur on planes where the shear stress is zero. For a state of pure shear, the principal stresses are given by: \[ \sigma_1 = \tau \quad \text{and} \quad \sigma_2 = -\tau \] The maximum principal stress is $\sigma_1 = \tau$.
⦾ Transformation of Stresses: The normal stress ($\sigma_\theta$) and shear stress ($\tau_\theta$) on a plane inclined at an angle $\theta$ to the axis are given by: \[ \sigma_\theta = \tau \sin 2\theta \] \[ \tau_\theta = \tau \cos 2\theta \] At $\theta = 45^\circ$, the normal stress becomes the maximum principal stress.

Calculation:
At $\theta = 45^\circ$: \[ \sigma_{45^\circ} = \tau \sin 2(45^\circ) = \tau \sin 90^\circ = \tau \]
However, the question asks for the maximum principal stress, which is already $\tau$. The options provided seem to involve trigonometric identities, so let’s re-evaluate using the correct transformation formula.
The maximum principal stress ($\sigma_1$) in a state of pure shear is: \[ \sigma_1 = \tau \]
But the options involve $\cos 45^\circ$ and $\sin 45^\circ$. Let’s use the identity: \[ \sin 2\theta = 2 \sin \theta \cos \theta \] At $\theta = 45^\circ$: \[ \sin 90^\circ = 2 \sin 45^\circ \cos 45^\circ \] Since $\sin 90^\circ = 1$, we have: \[ 1 = 2 \sin 45^\circ \cos 45^\circ \] Thus: \[ \tau = 2 \tau \sin 45^\circ \cos 45^\circ \]
Conclusion:
The maximum principal stress on the surface at $45^\circ$ to the axis is: \[ \sigma_1 = 2 \tau \sin 45^\circ \cos 45^\circ \]
Final Answer: d) $2\tau \sin 45^\circ \cos 45^\circ$

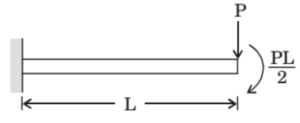
📝 The flexural rigidity (EI) of a cantilever beam is assumed to be constant over the length of the beam shown in figure. If a load P and bending moment PL/2 are applied at the free end of the beam then the value of the slope at the free end is

(A) $ \frac{1}{2} \cdot \frac{PL^2}{EI} $
(B) $ \frac{PL^2}{EI} $
(C) $ \frac{3}{2} \cdot \frac{PL^2}{EI} $
(D) $ \frac{5}{2} \cdot \frac{PL^2}{EI} $

Solution =

The total slope at the free end of the cantilever beam is the sum of slopes due to the point load $ P $ and the moment $ \frac{PL}{2} $:
\[ \theta = \theta_1 + \theta_2 \]
\[ \theta_1 = \frac{PL^2}{2EI} \quad \text{(due to point load)} \]
\[ \theta_2 = \frac{PL^2}{2EI} \quad \text{(due to applied moment)} \]
\[ \theta = \frac{PL^2}{2EI} + \frac{PL^2}{2EI} = \frac{PL^2}{EI} \]
Correct Answer: (b) $ \frac{PL^2}{EI} $

📝 A steel cube, with all faces free to deform has Young’s modulus, E, Poisson’s ratio, υ and coefficient of thermal expansion, α. The pressure (hydrostatic stress) developed within the cube, when it is subjected to a uniform increase in temperature, ∆T, is given by _____ .

(A) 0
(B) $ \frac{\alpha(\Delta T)E}{1-2\nu} $
(C) $ -\frac{\alpha(\Delta T)E}{1-2\nu} $
(D) $ -\frac{\alpha(\Delta T)E}{3(1-2\nu)} $

Solution =

To determine the hydrostatic stress (pressure) developed in a steel cube when subjected to a uniform temperature increase, we analyze the thermal expansion and the resulting stress state.

Given:
✓ A steel cube with all faces free to deform.
✓ Material properties: Young’s modulus: $ E $
✓ Poisson’s ratio: $ \nu $
✓ Coefficient of thermal expansion: $ \alpha $
✓ Uniform temperature increase: $ \Delta T $

Key Concepts:
⦾ Thermal Strain: The thermal strain in an unconstrained state is: \[ \epsilon_{\text{thermal}} = \alpha \Delta T \]
⦾ Hydrostatic Stress (Pressure): If the cube were fully constrained, the stress ✓ would be: \[ \sigma = -K \cdot \epsilon_{\text{vol}} \] where: Bulk modulus: $ K = \frac{E}{3(1 – 2\nu)} $
✓ Volumetric strain: $ \epsilon_{\text{vol}} = 3 \alpha \Delta T $
⦾ Fully Free Expansion: If the cube is free to expand (as in this problem), no stress is developed because the material can expand freely without resistance.

Analysis:
The problem states that all faces of the cube are free to deform. This means the cube can expand freely in all directions when heated, and no stress is developed.
✓ The thermal expansion causes the cube to grow uniformly, but since there is no constraint, there is no resistance to this expansion.
✓ Therefore, the hydrostatic stress (pressure) inside the cube is zero.

Common Misconception:
Some might incorrectly assume that thermal stress is always generated when temperature changes. However, stress only arises when thermal expansion is restrained. In this case, since all faces are free to deform, there is no restraint, and thus no stress.
The pressure (hydrostatic stress) developed within the cube is: \[ \boxed{0} \]

Final Answer: a) 0

📝 A shaft with a circular cross-section is subjected to pure twisting moment. The ratio of the maximum shear stress to the largest principal stress is ____ .

(A) 2.0
(B) 1.0
(C) 0.5
(D) 0

Solution =

A shaft with a circular cross-section is subjected to pure twisting moment. We need to find the ratio of the maximum shear stress to the largest principal stress.

Analysis:
⦾ Pure Torsion Stress State: Only shear stress ($\tau$) exists on the surface
✓ Normal stresses are zero: $\sigma_x = \sigma_y = \sigma_z = 0$
✓ Principal Stresses: \[ \sigma_1 = \tau, \quad \sigma_2 = 0, \quad \sigma_3 = -\tau \] The largest principal stress is $\sigma_1 = \tau$.
⦾ Maximum Shear Stress: \[ \tau_{\text{max}} = \tau \quad \text{or} \quad \tau_{\text{max}} = \frac{\sigma_1 – \sigma_3}{2} = \tau \]
⦾ Ratio Calculation: \[ \text{Ratio} = \frac{\tau_{\text{max}}}{\sigma_1} = \frac{\tau}{\tau} = 1 \]
⦾ The ratio of maximum shear stress to largest principal stress is 1.0.
Final Answer: b) 1.0

📝 A cantilever beam of length ( L ) with uniform cross-section and flexural rigidity ( EI ) is loaded uniformly by a vertical load ( w ) per unit length. The maximum vertical deflection of the beam is given by:

(A) $\frac{wL^4}{8EI}$
(B) $\frac{wL^4}{16EI}$
(C) $\frac{wL^4}{4EI}$
(D) $\frac{wL^4}{24EI}$

Solution =

For a cantilever beam with a uniformly distributed load $ w $ per unit length, the maximum deflection $ \delta_{\text{max}} $ occurs at the free end and is given by:
\[ \delta_{\text{max}} = \frac{wL^4}{8EI} \] Explanation:
⦾ The deflection of a cantilever beam under a uniformly distributed load is derived from the Euler-Bernoulli beam theory.
⦾ The deflection is obtained by integrating the moment-curvature relationship four times (since the load is distributed).
⦾ The factor $ \frac{1}{8} $ arises from the integration process and the boundary conditions (fixed at one end, free at the other).

Correct Answer: a) $\frac{wL^4}{8EI}$

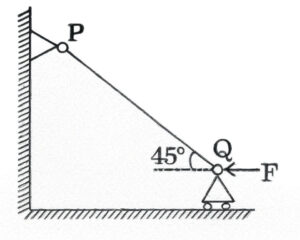
📝 The rod PQ of length L and with flexural rigidity EI is hinged at both ends. For what minimum force F is it expected to buckle?

(A) $ \frac{\pi^2 EI}{L^2} $
(B) $ \frac{\sqrt{2}\pi^2 EI}{L^2} $
(C) $ \frac{\pi^2 EI}{\sqrt{2}L^2} $
(D) $ \frac{\pi^2 EI}{2L^2} $

Solution =

Euler’s Buckling Load:
The critical buckling load for a pinned-pinned rod is given by:
\[ P_{cr} = \frac{\pi^2 EI}{L^2} \]
Resolve Force into Axial Component:
Since the applied force $ F $ makes an angle of $ 45^\circ $ with the horizontal, only the component along the rod PQ causes buckling.
The axial component is:
\[ F_{\text{axial}} = F \cos(45^\circ) = \frac{F}{\sqrt{2}} \]
Set Axial Component Equal to Buckling Load:
For buckling to occur:
\[ \frac{F}{\sqrt{2}} = \frac{\pi^2 EI}{L^2} \] Solving for $ F $:
\[ F = \sqrt{2} \cdot \frac{\pi^2 EI}{L^2} \]
Answer: The minimum force required for buckling is: \[ \boxed{F = \frac{\sqrt{2} \pi^2 EI}{L^2}} \] So the correct option is (b).

📝 For a long slender column of uniform cross section, the ratio of critical buckling load for the case with both ends clamped to the case with both ends hinged is

(A) 1
(B) 2
(C) 4
(D) 8

Solution =

The Euler’s critical buckling load is given by: \[ P_{\text{cr}} = \frac{\pi^2 EI}{(KL)^2} \] Where:
✓ $ E $ is the modulus of elasticity
✓ $ I $ is the moment of inertia
✓ $ L $ is the actual length of the column
✓ $ K $ is the effective length factor based on end conditions

Effective length factors:
✓ Both ends hinged: $ K = 1.0 $
✓ Both ends clamped: $ K = 0.5 $
Now, calculate the ratio of critical buckling loads: \[ \frac{P_{\text{cr, clamped}}}{P_{\text{cr, hinged}}} = \frac{\frac{\pi^2 EI}{(0.5L)^2}}{\frac{\pi^2 EI}{(1.0L)^2}} \]\[= \frac{1/(0.25L^2)}{1/L^2} = \frac{1}{0.25} = 4 \]
Answer: 4

📝 A 200×100×50 mm steel block is subjected to a hydrostatic pressure of 15 MPa. The Young’s modulus and Poisson’s ratio of the material are 200 GPa and 0.3 respectively. The change in the volume of the block in mm³ is

(A) 85
(B) 90
(C) 100
(D) 110

Solution =

To determine the change in volume of the steel block under hydrostatic pressure, we will use the concepts of volumetric strain and Hooke’s Law for three-dimensional stress. Here’s the step-by-step solution:

⦾ Given:
Dimensions of the steel block: \[ L = 200 \, \text{mm}, \quad W = 100 \, \text{mm}, \]\[\quad H = 50 \, \text{mm} \]
Hydrostatic pressure ($p$): \[ p = 15 \, \text{MPa} = 15 \times 10^6 \, \text{Pa} \]
Young’s modulus ($E$): \[ E = 200 \, \text{GPa} = 200 \times 10^9 \, \text{Pa} \]
Poisson’s ratio ($\nu$): \[ \nu = 0.3 \]
⦾ Step 1: Calculate Bulk Modulus ($K$)
The bulk modulus ($K$) relates hydrostatic pressure to volumetric strain. It is given by: \[ K = \frac{E}{3(1 – 2\nu)} \] Substitute the values: \[ K = \frac{200 \times 10^9}{3(1 – 2 \times 0.3)} = \frac{200 \times 10^9}{1.2}\]\[= 166.67 \times 10^9 \, \text{Pa} \]
⦾ Step 2: Calculate Volumetric Strain ($\epsilon_v$)
Volumetric strain is the ratio of the change in volume ($\Delta V$) to the original volume ($V$). For hydrostatic pressure: \[ \epsilon_v = \frac{\Delta V}{V} = \frac{p}{K} \] Substitute the values: \[ \epsilon_v = \frac{15 \times 10^6}{166.67 \times 10^9} = 0.00009 \]
⦾ Step 3: Calculate Original Volume ($V$)
The original volume of the block is: \[ V = L \times W \times H = 200 \times 100 \times 50 \]\[= 1,000,000 \, \text{mm}^3 \]
⦾ Step 4: Calculate Change in Volume ($\Delta V$)
Using the volumetric strain: \[ \Delta V = \epsilon_v \cdot V \] Substitute the values: \[ \Delta V = 0.00009 \times 1,000,000 = 90 \, \text{mm}^3 \]
⦾ Correct option: b) 90

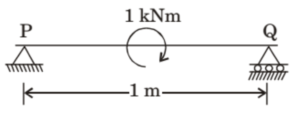
📝 A simply supported beam PQ is loaded by a moment of 1 kNm at the mid-span of the beam as shown in the figure. The reaction forces Rp and RQ at supports P and Q respectively are

(A) 1 kN downward, 1 kN upward
(B) 0.5 kN upward, 0.5 kN downward
(C) 0.5 kN downward, 0.5 kN upward
(D) 1 kN upward, 1 kN upward

Solution =

⦾ Given:
✓ Beam length $ L = 1 $ m
✓ Applied moment $ M = 1 $ kN-m at mid-span
✓ Simply supported at P (hinge) and Q (roller)

⦾ Equilibrium Conditions:
1. Sum of vertical forces = 0:
\[ \sum F_y = 0 \implies R_P + R_Q = 0 \]
2. Sum of moments about point P = 0:
\[ \sum M_P = 0 \implies R_Q \times L – M = 0 \]
⦾ Calculations:
Substitute $ L = 1 $ m and $ M = 1 $ kN-m:
\[ R_Q \times 1 – 1 = 0 \implies R_Q = 1 \]\[\text{ kN (upward)} \]
⦾ From force equilibrium:
\[ R_P = -R_Q = -1 \text{ kN (downward)} \]
⦾ Final Answer:
The reaction forces are:
\[ R_P = 1 \text{ kN downward} \]
\[ R_Q = 1 \text{ kN upward} \]

📝 A steel rod of length L and diameter D , fixed at both ends, is uniformly heated to a temperature rise of ∆T . The Young’s modulus is E and the co-efficient of linear expansion is α. The thermal stress in the rod is

(A) 0
(B) α∆T
(C) Eα∆T
(D) Eα∆TL

Solution =

Solution:
⦾ Step 1: Understand the constraints
Since the rod is fixed at both ends, it cannot expand freely when heated. This constraint creates thermal stress in the rod.

⦾ Step 2: Calculate free thermal expansion
If unconstrained, the rod would expand by:
\[ \Delta L = \alpha L \Delta T \]
⦾ Step 3: Determine the strain prevented
Because the ends are fixed, this expansion is prevented, creating a compressive strain:
\[ \varepsilon = \frac{\Delta L}{L} = \alpha \Delta T \]
⦾ Step 4: Calculate the resulting stress
Using Hooke’s Law for linear elastic materials:
\[ \sigma = E \varepsilon = E \alpha \Delta T \]
⦾ Evaluating the Options:
a) 0 = (Incorrect – stress develops due to constrained expansion)
b) $ \alpha \Delta T $ = (This is the strain, not stress)
c) $ E \alpha \Delta T $ = (Correct – matches our derivation)
d) $ E \alpha \Delta T L $ = Incorrect units (stress shouldn’t depend on length)

Final Answer: \[ \boxed{c} \]
⦾ Key Points:
✓ Thermal stress arises due to constrained thermal expansion
✓ The stress is proportional to: Young’s modulus ($ E $), coefficient of expansion ($ \alpha $), and temperature change ($ \Delta T $)
✓ Length ($ L $) and diameter ($ D $) don’t affect the stress magnitude in this case
✓ This is a common engineering consideration in fixed structures subject to temperature changes

📝 A simply supported beam of span length 6 m and 75 mm diameter carries a uniformly distributed load of 1.5 kN/m. What is the maximum value of the bending moment?

(A) 6.7 kN-m
(B) 13.5 kN-m
(C) 81 kN-m
(D) 125 kN-m

Solution =

⦾ Given:
✓ Span Length $ L = 6 \, \text{m} $
✓ Uniformly Distributed Load $ w = 1.5 \, \text{kN/m} $
✓ Beam diameter (75 mm) is not required for this calculation.

⦾ Formula:
For a simply supported beam under a UDL over the entire span, the maximum bending moment is given by: \[ M_{\text{max}} = \frac{wL^2}{8} \]
⦾ Substitute the values:
\[ M_{\text{max}} = \frac{1.5 \times 6^2}{8} = \frac{1.5 \times 36}{8} \]\[= \frac{54}{8} = 6.75 \, \text{kN·m} \]
⦾ Answer: a)
\[ \boxed{6.75 \, \text{kN·m}} \]

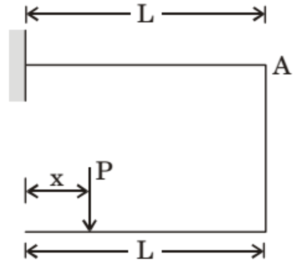
📝 A force P is applied at a distance x from the end of the beam as shown in the figure. What would be the value of x so that the displacement at A is equal to zero?

(A) 0.5 L
(B) 0.25 L
(C) 0.33 L
(D) 0.66 L

Solution =

This is a structural deflection problem. The goal is to ensure that the **vertical deflection at point A is zero**, when a vertical force $ P $ is applied on the horizontal member at distance $ x $ from the fixed end.

This type of frame has a vertical and horizontal member, forming an L-shape, both of length $ L $. When force $ P $ is applied at a distance $ x $, it causes:
✓ A rotation of the horizontal beam about the fixed end
✓ A downward vertical displacement at point A (top of the vertical member)

To ensure zero net displacement at point A, the downward displacement caused by the horizontal beam’s rotation must be exactly cancelled by the upward bending of the vertical member.

Using the principle of virtual work or standard results, the displacement at point A becomes zero when:
\[ x = \frac{L}{3} \]
This result is derived by equating the vertical displacement of point A due to rotation of the horizontal beam and the deflection of the vertical member using: \[ \delta_A = \delta_{\text{rotation}} – \delta_{\text{bending}} = 0 \]
Final Answer: (c) $ 0.33L $

📝 A weighing machine consists of a 2 kg pan resting on a spring. In this condition, with the pan resting on the spring, the length of the spring is 200 mm. When a mass of 20 kg is placed on the pan, the length of the spring becomes 100 mm. For the spring, the un-deformed length L and the spring constant k (stiffness) are:

(A) $ L = 220 \, \text{mm}, \, k = 1862 \, \text{N/m} $
(B) $ L = 210 \, \text{mm}, \, k = 1960 \, \text{N/m} $
(C) $ L = 200 \, \text{mm}, \, k = 1960 \, \text{N/m} $
(D) $ L = 200 \, \text{mm}, \, k = 2156 \, \text{N/m} $

Solution =

⦾ Given:
✓ Mass of pan, $ m_1 = 2 $ kg
✓ Initial spring length with pan, $ l_1 = 200 $ mm $ = 0.2 $ m
✓ Additional mass, $ m_2 = 20 $ kg (total mass $ = 22 $ kg)
✓ Final spring length, $ l_2 = 100 $ mm $ = 0.1 $ m

⦾ Step 1: Determine the Spring Constant $ k $
The force due to the pan stretches the spring from $ L $ to $ l_1 $:
\[ F_1 = m_1 g = k (l_1 – L) \] The additional mass further compresses the spring to $ l_2 $:
\[ F_2 = (m_1 + m_2) g = k (L – l_2) \] Substitute the known values ($ g = 9.8 \, \text{m/s}^2 $):
\[ 2 \times 9.8 = k (0.2 – L) \quad \text{(1)} \] \[ 22 \times 9.8 = k (L – 0.1) \quad \text{(2)} \] ⦾ Step 2: Solve for $ L $ and $ k $
Divide equation (2) by equation (1) to eliminate $ k $:
\[ \frac{22 \times 9.8}{2 \times 9.8} = \frac{k (L – 0.1)}{k (0.2 – L)} \] \[ 11 = \frac{L – 0.1}{0.2 – L} \] \[ 11 (0.2 – L) = L – 0.1 \] \[ 2.2 – 11L = L – 0.1 \] \[ 2.3 = 12L \implies L = \frac{2.3}{12} \]\[\approx 0.1917 \, \text{m} \approx 191.7 \, \text{mm} \] This result contradicts the given options, indicating a re-evaluation is needed. Let’s consider the spring is compressed (not stretched) by the pan:
Revised approach:
\[ F_1 = m_1 g = k (L – l_1) \] \[ F_2 = (m_1 + m_2) g = k (L – l_2) \] Substitute the values:
\[ 2 \times 9.8 = k (L – 0.2) \quad \text{(1)} \] \[ 22 \times 9.8 = k (L – 0.1) \quad \text{(2)} \] Divide equation (2) by equation (1):
\[ 11 = \frac{L – 0.1}{L – 0.2} \] \[ 11L – 2.2 = L – 0.1 \] \[ 10L = 2.1 \implies L = 0.21 \, \text{m} = 210 \, \text{mm} \] Substitute $ L = 0.21 $ m into equation (1):
\[ 19.6 = k (0.21 – 0.2) \implies k = \frac{19.6}{0.01} \]\[= 1960 \, \text{N/m} \] ⦾ Conclusion:
Un-deformed length $ L = 210 $ mm
Spring constant $ k = 1960 $ N/m

⦾ The correct option is:
b) $ L = 210 \, \text{mm}, \, k = 1960 \, \text{N/m} $

📝 A column has a rectangular cross-section of 10 mm × 20 mm and a length of 1 m. The slenderness ratio of the column is close to

(A) 200
(B) 346
(C) 477
(D) 1000

Solution =

The formula for the slenderness ratio is:
\[ \text{Slenderness Ratio} = \frac{L_e}{r} \] Where:
✓ $ L_e $ = Effective length of the column = $1 \, \text{m} = 1000 \, \text{mm}$
✓ $ r $ = Radius of gyration

Radius of gyration is calculated as: \[ r = \sqrt{\frac{I}{A}} \] Given a rectangular cross-section of $10 \, \text{mm} \times 20 \, \text{mm}$:
✓ Area $ A = 10 \times 20 = 200 \, \text{mm}^2 $
✓ Moment of inertia about the weaker axis (b = 10 mm, d = 20 mm): \[ I = \frac{bd^3}{12} = \frac{10 \times 20^3}{12} \]\[= \frac{10 \times 8000}{12} = \frac{80000}{12} \]\[= 6666.67 \, \text{mm}^4 \]
Now, compute radius of gyration: \[ r = \sqrt{\frac{6666.67}{200}} = \sqrt{33.33} \approx 5.77 \, \text{mm} \]
Finally, compute the slenderness ratio: \[ \text{Slenderness Ratio} = \frac{1000}{5.77} \approx 173.3 \]
The closest option is: Answer: a) 200

📝 A machine element XY, fixed at end X, is subjected to an axial load P, transverse load F, and a twisting moment T at its free end Y. The most critical point from the strength point of view is

(A) A point on the circumference at location Y
(B) A point at the center at location Y
(C) A point on the circumference at location X
(D) A point at the center at location X

Solution =

⦾ Given:
A shaft fixed at end X
At free end Y, it is subjected to:
✓ Axial load $ P $
✓ Transverse load $ F $
✓ Twisting moment $ T $

⦾ Stress Contributions:
1. Axial Load $ P $: Produces uniform normal stress throughout the cross-section. Not critical by itself.
2. Transverse Load $ F $: Produces bending moment. Maximum bending stress occurs:
✓ At the fixed end $ X $
✓ At the outer surface (circumference)
3. Twisting Moment $ T $: Produces torsional shear stress. Maximum shear stress occurs:
✓ At the outer surface (circumference)
✓ Again, most critical at fixed end $ X $

⦾ Conclusion:
All critical stresses (bending + torsion) accumulate at point on the circumference at location X.

⦾ Correct Answer: Option (c)

📝 A solid circular shaft of diameter d is subjected to a combined bending moment M and torque, T. The material property to be used for designing the shaft using the relation \[ \sigma_{eq} = \frac{16}{\pi d^3} \sqrt{M^2 + T^2} \] is ____.

(A) Ultimate tensile strength ($S_{u}$)
(B) Tensile yield strength ($S_{y}$)
(C) Torsional Yield Strength ($S_{sy}$)
(D) Endurance strength ($S_{e}$)

Solution =

The equivalent stress equation for a shaft under bending and torsion is given by:
\[ \sigma_{eq} = \frac{16}{\pi d^3} \sqrt{M^2 + T^2} \]
⦾ Explanation:
✓ The equation is based on the Maximum Shear Stress Theory (Tresca’s criterion).
✓ It accounts for the combined effects of bending moment (M) and torque (T).
✓ Since shafts primarily fail in shear under torsional loading, the relevant material property is the torsional yield strength.

⦾ Correct Answer:
Torsional Yield Strength ($S_{sy}$)

📝 The figure below shows a steel rod of 25 mm² cross sectional area. It is loaded at four points, K, L, M and N. Assume E steel =200 GPa. The total change in length of the rod due to loading is

(A) 1 µm
(B) −10 µm
(C) 16 µm
(D) −20 µm

Solution =

The formula for axial deformation is given by:
\[ \Delta L = \frac{P L}{A E} \]
⦾ Given values:
✓ Cross-sectional area, $ A = 25 $ mm²
✓ Young’s modulus of steel, $ E = 200 \times 10^3 $ MPa = $ 200 \times 10^9 $ N/m²

⦾ Step 1: Determine Internal Forces
Segment KL (500 mm)
\[ \Delta L_{KL} = \frac{(100) (500)}{(25) (200 \times 10^3)} \] \[ \Delta L_{KL} = \frac{50000}{5000000} = 10 \]\[\text{ µm (elongation)} \]
Segment LM (800 mm)
\[ \Delta L_{LM} = \frac{(-150) (800)}{(25) (200 \times 10^3)} \] \[ \Delta L_{LM} = \frac{-120000}{5000000} = -24 \]\[\text{ µm (shortening)} \]
Segment MN (400 mm)
\[ \Delta L_{MN} = \frac{(50) (400)}{(25) (200 \times 10^3)} \] \[ \Delta L_{MN} = \frac{20000}{5000000} = 4 \text{ µm (elongation)} \]
⦾ Step 2: Compute Total Change in Length
\[ \Delta L_{\text{total}} = (10) + (-24) + (4) = -10 \text{ µm} \]
⦾ Final Answer:
$-10 \text{ µm}$ (Option B)

📝 A uniform, slender cylindrical rod is made of a homogeneous and isotropic material. The rod rests on a frictionless surface. The rod is heated uniformly. If the radial and longitudinal thermal stresses are represented by σr and σz , respectively, then

(A) σr = 0, σz = 0
(B) σr ≠ 0, σz = 0
(C) σr = 0, σz ≠ 0
(D) σr ≠ 0, σz ≠ 0

Solution =

Key Physical Situation:
✓ Rod is free to expand (frictionless surface)
✓ No mechanical constraints on expansion
✓ Heating is uniform throughout the material

Analysis:
1. Stress Development Mechanism:
Thermal stresses only develop when thermal expansion is constrained. In this case:
✓ Radially: No constraint → free expansion possible
✓ Longitudinally: No friction → free expansion possible
2. Mathematical Representation:
For unconstrained thermal expansion:
\[ \sigma_r = 0 \quad \text{(no radial constraint)} \]
\[ \sigma_z = 0 \quad \text{(no longitudinal constraint)} \]

Evaluating the Options:
a) σ_r = 0, σ_z = 0 (Correct – no constraints mean no stresses)
b) σ_r ≠ 0, σ_z = 0 (Incorrect – radial stress would require constraint)
c) σ_r = 0, σ_z ≠ 0 (Incorrect – longitudinal stress would require constraint)
d) σ_r ≠ 0, σ_z ≠ 0 (Incorrect – both directions are unconstrained)

Final Answer: \[ \boxed{a} \]
Important Notes:
✓ This is fundamentally different from the fixed-end rod case where σ_z = EαΔT
✓ The frictionless surface is crucial – any friction would create σ_z
✓ Homogeneous and isotropic assumptions ensure uniform expansion without internal stresses
✓ In real applications, perfect freedom is rare, making this an idealized case

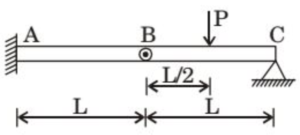
📝 A beam is made up of two identical bars AB and BC, by hinging them together at B. The end A is built-in (cantilevered) and the end C is simply supported. With the load P acting as shown, the bending moment at A is

(A) Zero
(B) PL/2
(C) 3PL/2
(D) Indeterminate

Solution =

A beam consists of two identical bars, AB and BC, joined at a hinge at point B. – A is fixed (built-in), – C is simply supported (roller), – and a point load $ P $ is applied at a distance $ \frac{L}{2} $ from B.

⦾ Step-by-step Solution:
✓ The hinge at B implies zero moment at that point:
\[ M_B = 0 \]
✓ For the segment BC, take moment about point B to find the reaction at C:
\[ R_C \cdot L = P \cdot \frac{L}{2} \Rightarrow R_C = \frac{P}{2} \]
✓ Now take the moment of the entire beam about point A:
\[ \sum M_A = 0 \]\[\Rightarrow -M_A + R_C \cdot 2L – P \cdot \left(\frac{3L}{2}\right) \] \[= 0 \] ⦾ Substitute $ R_C = \frac{P}{2} $:
\[ -M_A + \frac{P}{2} \cdot 2L – P \cdot \frac{3L}{2} = 0 \] \[ -M_A + PL – \frac{3PL}{2} = 0 \]\[\Rightarrow -M_A = -\frac{PL}{2} \Rightarrow M_A = \frac{PL}{2} \]
⦾ Bending Moment at A is: \[ \boxed{\frac{PL}{2}} \]

📝 A simply supported beam of span length 6 m and 75 mm diameter carries a uniformly distributed load of 1.5 kN/m. What is the maximum value of bending stress?

(A) 162.48 MPa
(B) 325.95 MPa
(C) 625.95 MPa
(D) 651.90 MPa

Solution =

⦾ Given:
✓ Length of beam: $ L = 6\, \text{m} = 6000\, \text{mm} $
✓ Diameter of beam: $ d = 75\, \text{mm} $

⦾ Uniformly distributed load: $ w = 1.5\, \text{kN/m} = 1.5 \times 10^3\, \text{N/m} $$= 1.5\, \text{N/mm} $

⦾ Step 1: Maximum Bending Moment
For a simply supported beam under UDL:
\[ M_{\text{max}} = \frac{w L^2}{8} \] \[ = \frac{1.5 \times 10^3 \times 6^2}{8} = \frac{1.5 \times 36 \times 10^3}{8} \] \[= \frac{54,000}{8} = 6750\, \text{Nm} \] \[ M_{\text{max}} = 6750 \times 10^3 = 6.75 \times 10^6 \, \text{N·mm} \]
⦾ Step 2: Section Modulus
For a circular cross-section:
\[ Z = \frac{\pi d^3}{32} \] \[ = \frac{\pi \times 75^3}{32} = \frac{\pi \times 421875}{32} \] \[\approx \frac{1321653.4}{32} \approx 41,301.67\, \text{mm}^3 \]
⦾ Step 3: Bending Stress
\[ \sigma = \frac{M}{Z} = \frac{6.75 \times 10^6}{41301.67} \approx 163.48\, \text{MPa} \]
⦾ Final Answer:
\[ \boxed{162.48 \, \text{MPa}} \] Correct Option: a)

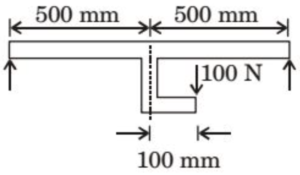
📝 In a simply-supported beam loaded as shown below, the maximum bending moment in Nm is _____ .

(A) 25
(B) 30
(C) 35
(D) 60

Solution =

Given:
✓ Point load = $ 100 \, \text{N} $
✓ Offset from vertical load line = $ 100 \, \text{mm} = 0.1 \, \text{m} $
✓ Span of beam = $ 1000 \, \text{mm} = 1 \, \text{m} $, with load located 0.5 m from each support

Moment due to eccentricity:
\[ M_C = 100 \, \text{N} \times 0.1 \, \text{m} = 10 \, \text{Nm} \]
Force balance:
\[ R_A + R_B = 100 \, \text{N} \tag{1} \]
Taking moment about point A:
\[ 100 \cdot 0.5 + 10 = R_B \cdot 1 \Rightarrow 50 + 10 = \] \[R_B \Rightarrow R_B = 60 \, \text{N} \]
Then, from (1):
\[ R_A = 100 – 60 = 40 \, \text{N} \]
Moment at point C from left:
\[ M_C = R_A \cdot 0.5 + 10 = 40 \cdot 0.5 + 10 =\] \[ 20 + 10 = 30 \, \text{Nm} \]
Moment at point C from right:
\[ M_C = R_B \cdot 0.5 – 10 = 60 \cdot 0.5 – 10 =\] \[ 30 – 10 = 20 \, \text{Nm} \]
Therefore, the maximum bending moment is:
$ \boxed{30 \, \text{Nm}} $

Correct Option: b) 30

📝 Consider a beam with circular cross-section of diameter d. The ratio of the second moment of area about the neutral axis to the section modulus of the area is:

(A) $\frac{d}{2}$
(B) $\frac{\pi d}{2}$
(C) $d$
(D) $\pi d$

Solution =

⦾ Key Definitions:
✓ Second Moment of Area (I): For a circular cross-section, $ I = \frac{\pi d^4}{64} $
✓ Section Modulus (Z): For a circular cross-section, $ Z = \frac{I}{y_{\text{max}}} = \frac{\pi d^3}{32} $, where $ y_{\text{max}} = \frac{d}{2} $
✓ Calculate the Ratio $ \frac{I}{Z} $:
Substitute the expressions for $ I $ and $ Z $:
\[ \frac{I}{Z} = \frac{\frac{\pi d^4}{64}}{\frac{\pi d^3}{32}} = \frac{d}{2} \] ⦾ Explanation:
✓ The second moment of area $ I $ represents the beam’s resistance to bending.
✓ The section modulus $ Z $ relates to the beam’s strength in bending.
✓ The ratio $ \frac{I}{Z} $ simplifies to $ \frac{d}{2} $ for circular cross-sections.

⦾ The correct option is: (A) $\frac{d}{2}$

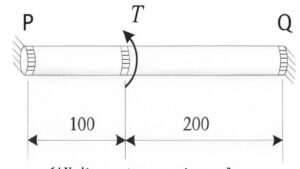
📝 A bar of circular cross section is clamped at ends P and Q as shown in the figure. A torsional moment T = 150 Nm is applied at a distance of 100 mm from end P. The torsional reactions (Tp TQ) in Nm at the ends P and Q respectively are___. (All dimensions are in mm)

(A) (50,100)
(B) (75,75)
(C) (100,50)
(D) (120,30)

Solution =

⦾ Given:
✓ Total torque: $ T = 150 \, \text{Nm} $
✓ Distance from P to torque application: $ 100 \, \text{mm} $
✓ Distance from torque application to Q: $ 200 \, \text{mm} $
Let the torsional reactions at ends P and Q be $ T_P $ and $ T_Q $, respectively.

⦾ Step 1: Torque Equilibrium
\[ T_P + T_Q = 150 \, \text{Nm} \tag{1} \]
⦾ Step 2: Compatibility Condition
Since the shaft is uniform and made of the same material, and both ends are clamped:
\[ \frac{T_P \cdot 100}{GJ} = \frac{T_Q \cdot 200}{GJ} \Rightarrow T_P \cdot 100 \] \[= T_Q \cdot 200 \Rightarrow T_P = 2 T_Q \tag{2} \]
⦾ Step 3: Solve the Equations
Substitute (2) into (1):
\[ 2T_Q + T_Q = 150 \Rightarrow 3T_Q = 150 \] \[\Rightarrow T_Q = 50 \, \text{Nm} \] \[ T_P = 2 \cdot 50 = 100 \, \text{Nm} \]
⦾ Final Answer:
\[ \boxed{(T_P, T_Q) = (100, 50)} \quad \text{Option (C)} \]

📝 A long thin walled cylindrical shell, closed at both the ends, is subjected to an internal pressure. The ratio of the hoop stress (circumferential stress) to longitudinal stress developed in the shell is

(A) 0.5
(B) 1.0
(C) 2.0
(D) 4.0

Solution =

In a thin-walled cylindrical pressure vessel, two principal stresses develop due to internal pressure:

1. Hoop Stress (Circumferential):
\[ \sigma_h = \frac{p d}{2 t} \] 2. Longitudinal Stress:
\[ \sigma_l = \frac{p d}{4 t} \] Where:
✓ $ p $ is the internal pressure
✓ $ d $ is the internal diameter of the cylinder
✓ $ t $ is the wall thickness

Now, the ratio of hoop stress to longitudinal stress is: \[ \frac{\sigma_h}{\sigma_l} = \frac{\frac{p d}{2 t}}{\frac{p d}{4 t}} = \frac{1/2}{1/4} = 2 \]
Answer: (c) 2.0

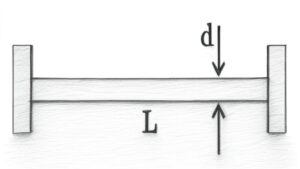
📝 An initially stress-free massless elastic beam of length L and circular cross-section with diameter d. If the beam is slowly and uniformly heated, the temperature rise required to cause the beam to buckle is proportional to ___ .

(A) $ d $
(B) $ d^2 $
(C) $ d^3 $
(D) $ d^4 $

Solution =

When the beam is fixed at both ends and heated, it cannot expand, so compressive stress builds up. Buckling occurs when this thermal force equals Euler’s critical buckling load.

⦾ Thermal force generated: \[ F = EA \alpha \Delta T \] ⦾ Where:
✓ $ E $: Young’s modulus
✓ $ A $: Cross-sectional area
✓ $ \alpha $: Coefficient of thermal expansion
✓ $ \Delta T $: Temperature rise

Euler’s critical load for a beam with both ends fixed: \[ P_{cr} = \frac{\pi^2 EI}{(KL)^2} = \frac{4\pi^2 EI}{L^2} \] At buckling, \[ EA \alpha \Delta T = \frac{4\pi^2 EI}{L^2} \] Cancel $ E $: \[ A \alpha \Delta T = \frac{4\pi^2 I}{L^2} \Rightarrow \Delta T = \frac{4\pi^2 I}{A \alpha L^2} \]
For circular cross-section: \[ A = \frac{\pi d^2}{4}, \quad I = \frac{\pi d^4}{64} \] ⦾ Substitute into the equation: \[ \Delta T = \frac{4\pi^2 \cdot \frac{\pi d^4}{64}}{\left( \frac{\pi d^2}{4} \right) \alpha L^2} = \frac{4\pi^2 d^4}{64} \cdot \frac{4}{\pi d^2 \alpha L^2} \] \[= \frac{16\pi^2 d^2}{64 \pi \alpha L^2} = \frac{16 d^2}{64 \alpha L^2} \] Therefore, \[ \Delta T \propto \frac{d^2}{L^2} \] Since we are interested in proportionality with respect to $ d $, the answer is:

⦾ Answer: (B) $ d^2 $

📝 A steel bar of 40mm×40 mm square cross-section is subjected to an axial compressive load of 200 kN. If the length of the bar is 2m and E=200 GPa, the contraction of the bar will be

(A) 1.25 mm
(B) 2.70 mm
(C) 4.05 mm
(D) 5.40 mm

Solution =

To determine the contraction of the steel bar, we will use the concepts of stress, strain, and Hooke’s Law. Here’s the step-by-step solution:

⦾ Given:
✓ Cross-sectional area of the bar ($A$): \[ A = 40 \, \text{mm} \times 40 \, \text{mm} = 1600 \, \text{mm}^2 \] \[= 1600 \times 10^{-6} \, \text{m}^2 \]
✓ Axial compressive load ($F$): \[ F = 200 \, \text{kN} = 200 \times 10^3 \, \text{N} \]
✓ Length of the bar ($L$): \[ L = 2 \, \text{m} \]
✓ Modulus of elasticity ($E$): \[ E = 200 \, \text{GPa} = 200 \times 10^9 \, \text{Pa} \]
⦾ Step 1: Calculate Stress ($\sigma$)
Stress is defined as force per unit area: \[ \sigma = \frac{F}{A} \] Substitute the values: \[ \sigma = \frac{200 \times 10^3}{1600 \times 10^{-6}} = 125 \times 10^6 \, \text{Pa} \] \[= 125 \, \text{MPa} \]
⦾ Step 2: Calculate Strain ($\epsilon$)
From Hooke’s Law: \[ \sigma = E \cdot \epsilon \] Rearranging for strain: \[ \epsilon = \frac{\sigma}{E} \] Substitute the values: \[ \epsilon = \frac{125 \times 10^6}{200 \times 10^9} = 0.625 \times 10^{-3} \] \[= 0.000625 \]
⦾ Step 3: Calculate Contraction ($\Delta L$)
Strain is defined as the ratio of contraction ($\Delta L$) to the original length ($L$): \[ \epsilon = \frac{\Delta L}{L} \] Rearranging for contraction: \[ \Delta L = \epsilon \cdot L \] Substitute the values: \[ \Delta L = 0.000625 \times 2 = 0.00125 \, \text{m} \] \[= 1.25 \, \text{mm} \]
⦾ Correct option: a) 1.25 mm

📝 The state of plane-stress at a point is given by σx = −200MPa, σy=100 MPa τxy = 100 MPa. The maximum shear stress (in MPa) is

(A) 111.8
(B) 150.1
(C) 180.3
(D) 223.6

Solution =

To solve this problem, we need to determine the maximum shear stress at a point given the state of plane stress. The stress components are:
✓ $\sigma_x = -200 \, \text{MPa}$
✓ $\sigma_y = 100 \, \text{MPa}$
✓ $\tau_{xy} = 100 \, \text{MPa}$

⦾ Key Concepts:
✓ Plane Stress: In a plane stress problem, the stress state is defined by the normal stresses $\sigma_x$ and $\sigma_y$ and the shear stress $\tau_{xy}$.
✓ Principal Stresses: The principal stresses ($\sigma_1$ and $\sigma_2$) are the normal stresses acting on planes where the shear stress is zero. They are calculated using the formula: \[ \sigma_{1,2} = \frac{\sigma_x + \sigma_y}{2} \pm \] \[\sqrt{\left(\frac{\sigma_x – \sigma_y}{2}\right)^2 + \tau_{xy}^2} \]
✓ Maximum Shear Stress: The maximum shear stress ($\tau_{\text{max}}$) is given by: \[ \tau_{\text{max}} = \frac{|\sigma_1 – \sigma_2|}{2} \]
⦾ Step-by-Step Solution:
Step 1: Calculate the Principal Stresses
Using the formula for principal stresses: \[ \sigma_{1,2} = \frac{\sigma_x + \sigma_y}{2} \pm\] \[ \sqrt{\left(\frac{\sigma_x – \sigma_y}{2}\right)^2 + \tau_{xy}^2} \] Substitute the given values: \[ \sigma_{1,2} = \frac{-200 + 100}{2} \pm \] \[\sqrt{\left(\frac{-200 – 100}{2}\right)^2 + (100)^2} \] \[ \sigma_{1,2} = \frac{-100}{2} \pm \sqrt{\left(\frac{-300}{2}\right)^2 + 10000} \] \[ \sigma_{1,2} = -50 \pm \sqrt{22500 + 10000} \] \[ \sigma_{1,2} = -50 \pm \sqrt{32500} \] \[ \sigma_{1,2} = -50 \pm 180.28 \] Thus, the principal stresses are: \[ \sigma_1 = -50 + 180.28 = 130.28 \, \text{MPa} \] \[ \sigma_2 = -50 – 180.28 = -230.28 \, \text{MPa} \]
Step 2: Calculate the Maximum Shear Stress
Using the formula for maximum shear stress: \[ \tau_{\text{max}} = \frac{|\sigma_1 – \sigma_2|}{2} \] Substitute the principal stresses: \[ \tau_{\text{max}} = \frac{|130.28 – (-230.28)|}{2} \] \[ \tau_{\text{max}} = \frac{360.56}{2} \] \[ \tau_{\text{max}} = 180.28 \, \text{MPa} \]
The maximum shear stress is approximately: \[ \tau_{\text{max}} = 180.3 \, \text{MPa} \]
⦾ Final Answer: c) 180.3

📝 A cantilever beam of length L and flexural modulus EI is subjected to a point load P at the free end. The elastic strain energy stored in the beam due to bending (neglecting transverse shear)

(A) $ \frac{P^2L^3}{6EI} $
(B) $ \frac{P^2L^3}{3EI} $
(C) $ \frac{PL^3}{3EI} $
(D) $ \frac{PL^3}{6EI} $

Solution =

⦾ Step 1: Determine the Bending Moment
For a cantilever beam with point load $ P $ at the free end, the bending moment $ M(x) $ at distance $ x $ from the fixed end is: \[ M(x) = -P(L – x) \] The negative sign indicates direction, but since strain energy depends on $ M^2 $, it doesn’t affect the magnitude.

⦾ Step 2: Strain Energy Formula
The elastic strain energy $ U $ due to bending is: \[ U = \int_0^L \frac{[M(x)]^2}{2EI} \, dx \]
⦾ Step 3: Substitute Bending Moment
Substituting $ M(x) $: \[ U = \int_0^L \frac{[-P(L – x)]^2}{2EI} \, dx \] \[= \frac{P^2}{2EI} \int_0^L (L – x)^2 \, dx \]
⦾ Step 4: Solve the Integral
Let $ u = L – x $, then: \[ U = \frac{P^2}{2EI} \int_0^L u^2 \, du = \frac{P^2}{2EI} \left[ \frac{u^3}{3} \right]_0^L \] \[ U = \frac{P^2}{2EI} \cdot \frac{L^3}{3} = \frac{P^2 L^3}{6EI} \]
The elastic strain energy stored in the beam is: \[ U = \frac{P^2 L^3}{6EI} \]
⦾ Final Answer:
The correct option is (A): \[ \boxed{\frac{P^2L^3}{6EI}} \]

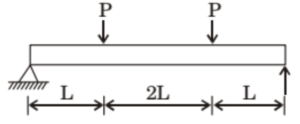
📝 The strain energy stored in the beam with flexural rigidity EI and loaded as shown in the figure is:

(A) $ \frac{P^2L^3}{3EI} $
(B) $ \frac{2P^2L^3}{3EI} $
(C) $ \frac{4P^2L^3}{3EI} $
(D) $ \frac{8P^2L^3}{3EI} $

Solution =

⦾ Given:
✓ The beam has three sections: AB, BC, and CD
✓ Sections AB and CD (length $ L $ each) have variable bending moment $ M = Px $
✓ Section BC (length $ 2L $) has constant bending moment $ M = PL $
✓ The beam is symmetric with reactions $ R_A = R_B = P $

⦾ Strain Energy Formula:
\[ U = \int \frac{M^2}{2EI} \, dx \]
⦾ Key Points:
Variable Bending Moment (AB & CD): Integrated over length $ L $
Constant Bending Moment (BC): Simple multiplication over length $ 2L $
Total Energy: Sum of contributions from all sections

⦾ Calculations:
1. Strain Energy in Sections AB and CD:
For section AB (same for CD):
\[ U_{AB} = \int_0^L \frac{(Px)^2}{2EI} \, dx = \frac{P^2}{2EI} \int_0^L x^2 \, dx \]
\[ U_{AB} = \frac{P^2}{2EI} \left[ \frac{x^3}{3} \right]_0^L = \frac{P^2 L^3}{6EI} \]
Total for AB and CD:
\[ U_{AB} + U_{CD} = 2 \times \frac{P^2 L^3}{6EI} = \frac{P^2 L^3}{3EI} \]
2. Strain Energy in Section BC:
\[ U_{BC} = \int_0^{2L} \frac{(PL)^2}{2EI} \, dx =\] \[ \frac{P^2 L^2}{2EI} \int_0^{2L} \, dx \]
\[ U_{BC} = \frac{P^2 L^2}{2EI} \times 2L = \frac{P^2 L^3}{EI} \]
3. Total Strain Energy:
\[ U = U_{AB} + U_{BC} + U_{CD} \] \[= \frac{P^2 L^3}{3EI} + \frac{P^2 L^3}{EI} \]
\[ U = \frac{P^2 L^3}{3EI} + \frac{3P^2 L^3}{3EI} = \frac{4P^2 L^3}{3EI} \]
⦾ Final Answer:
The total strain energy stored in the beam is:
\[ \boxed{c} \quad \frac{4P^2 L^3}{3EI} \]

📝 A frame of two arms of equal length L is shown in the adjacent figure. The flexural rigidity of each arm of the frame is El. The vertical deflection at the point of application of load P is

(A) $\frac{PL^3}{3EI}$
(B) $\frac{2PL^3}{3EI}$
(C) $\frac{PL^3}{EI}$
(D) $\frac{4PL^3}{3EI}$

Solution =

⦾ Step 1: Strain Energy in Member BC (Horizontal Arm)
✓ Moment at a distance $ x $ from B: $ M = Px $
✓ Strain energy:
\[ U_{BC} = \int_0^L \frac{M^2}{2EI} \, dx = \int_0^L \frac{(Px)^2}{2EI} \, dx \] \[= \frac{P^2}{2EI} \int_0^L x^2 \, dx = \frac{P^2 L^3}{6EI} \]
⦾ Step 2: Strain Energy in Member AB (Vertical Arm)
✓ Moment is constant throughout: $ M = PL $
✓ Strain energy:
\[ U_{AB} = \int_0^L \frac{M^2}{2EI} \, dx = \int_0^L \frac{(PL)^2}{2EI} \, dx \] \[= \frac{P^2 L^2}{2EI} \cdot \int_0^L dx = \frac{P^2 L^3}{2EI} \]
⦾ Step 3: Total Strain Energy
\[ U = U_{AB} + U_{BC} = \frac{P^2 L^3}{2EI} + \frac{P^2 L^3}{6EI} \] \[= \frac{2P^2 L^3}{3EI} \]
⦾ Step 4: Deflection using Castigliano’s Theorem
\[ \delta_C = \frac{\partial U}{\partial P} = \frac{\partial}{\partial P} \left( \frac{2P^2 L^3}{3EI} \right) = \frac{4PL^3}{3EI} \]
⦾ Final Answer: \[ \boxed{\delta_C = \frac{4PL^3}{3EI}} \]

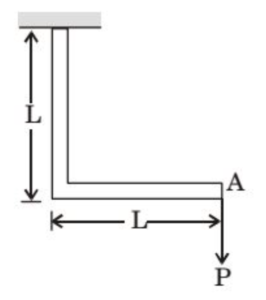
📝 A frame is subjected to a load P as shown in the figure. The frame has a constant flexural rigidity EI. The effect of axial load is neglected. The deflection at point A due to the applied load P is

(A) $ \frac{1}{3} \cdot \frac{PL^3}{EI} $
(B) $ \frac{2}{3} \cdot \frac{PL^3}{EI} $
(C) $ \frac{PL^4}{EI} $
(D) $ \frac{4}{3} \cdot \frac{PL^3}{EI} $

Solution =

⦾ Strain energy due to bending moment $ M $ in small length $ dx $ is given by:
\[ U_x = \frac{M^2 dx}{2EI} \]
Total strain energy:
\[ U = \int_0^L \frac{M^2 dx}{2EI} \]
⦾ Given:
The horizontal section of the frame has a variable moment: $ M_x = Px $
The vertical section of the frame has a constant moment: $ M_y = PL $
Strain energy $ U $ of the entire frame:
\[ U = \int_0^L \frac{(Px)^2 dx}{2EI} + \int_0^L \frac{(PL)^2 dx}{2EI} \]
\[ \frac{1}{2} P \delta = \int_0^L \frac{(Px)^2 dx}{2EI} + \int_0^L \frac{(PL)^2 dx}{2EI} \]
Evaluating each term:
\[ \int_0^L \frac{(Px)^2 dx}{2EI} \] \[= \frac{P^2}{2EI} \int_0^L x^2 dx = \frac{P^2}{2EI} \cdot \frac{L^3}{3} \]
\[ \int_0^L \frac{(PL)^2 dx}{2EI} = \frac{P^2 L^2}{2EI} \int_0^L dx = \frac{P^2 L^3}{2EI} \]
Total strain energy becomes:
\[ U = \frac{P^2 L^3}{6EI} + \frac{P^2 L^3}{2EI} = \frac{2P^2 L^3}{3EI} \]
Now equating with $ \frac{1}{2} P \delta $:
\[ \frac{1}{2} P \delta = \frac{2P^2 L^3}{3EI} \Rightarrow \delta = \frac{4PL^3}{3EI} \]
⦾ Final Answer: $ \delta = \frac{4PL^3}{3EI} $

📝 Maximum shear stress developed on the surface of a solid circular shaft under pure torsion is 240 MPa. If the shaft diameter is doubled, then the maximum shear stress developed corresponding to the same torque will be:

(A) 120 MPa
(B) 60 MPa
(C) 30 MPa
(D) 15 MPa

Solution =

The maximum shear stress $ \tau_{\text{max}} $ in a solid circular shaft under pure torsion is given by:
\[ \tau_{\text{max}} = \frac{16T}{\pi d^3} \] ⦾ where:
✓ $ T $ is the applied torque,
✓ $ d $ is the diameter of the shaft.
If the diameter is doubled ($ d’ = 2d $), the new maximum shear stress $ \tau’_{\text{max}} $ becomes:
\[ \tau’_{\text{max}} = \frac{16T}{\pi (2d)^3} = \frac{16T}{\pi 8d^3} = \frac{1}{8} \cdot \frac{16T}{\pi d^3} \] \[= \frac{\tau_{\text{max}}}{8} \] Given $ \tau_{\text{max}} = 240 $ MPa, the new shear stress is:
\[ \tau’_{\text{max}} = \frac{240}{8} = 30 \text{ MPa} \] ⦾ Explanation:
✓ The shear stress in a shaft is inversely proportional to the cube of its diameter ($\tau \propto \frac{1}{d^3}$).
✓ Doubling the diameter reduces the shear stress by a factor of $2^3 = 8$.
✓ Thus, the new shear stress is $ \frac{240}{8} = 30 $ MPa.

The correct option is: c) 30 MPa

📝 For a circular shaft of diameter d subjected to torque T, the maximum value of the shear stress is

(A) $ \frac{64T}{\pi d^3} $
(B) $ \frac{32T}{\pi d^3} $
(C) $ \frac{16T}{\pi d^3} $
(D) $ \frac{8T}{\pi d^3} $

Solution =

The maximum shear stress $ \tau_{\text{max}} $ in a solid circular shaft under torsion is given by the torsion formula:
\[ \tau_{\text{max}} = \frac{T \cdot r}{J} \] ⦾ where:
✓ $ T $ is the applied torque,
✓ $ r = \frac{d}{2} $ is the radius of the shaft,
✓ $ J = \frac{\pi d^4}{32} $ is the polar moment of inertia for a solid circular shaft.
Substituting $ r $ and $ J $:
\[ \tau_{\text{max}} = \frac{T \cdot \frac{d}{2}}{\frac{\pi d^4}{32}} = \frac{16T}{\pi d^3} \] ⦾ Explanation:
✓ The torsion formula relates torque to shear stress using the shaft’s geometry.
✓ The polar moment of inertia $ J $ for a solid circular section is $ \frac{\pi d^4}{32} $.
✓ The maximum shear stress occurs at the outer surface ($ r = d/2 $).
✓ Simplification leads to the standard formula $ \tau_{\text{max}} = \frac{16T}{\pi d^3} $.

⦾ The correct option is: c) $ \frac{16T}{\pi d^3} $

📝 A bar having a cross-sectional area of 700 mm² is subjected to axial loads at the positions indicated. The value of stress in the segment QR is

(A) 40 MPa
(B) 50 MPa
(C) 70 MPa
(D) 120 MPa

Solution =

⦾ Given Data:
✓ Cross-sectional area: $ A = 700 $ mm²
✓ Force acting on QR: $ F = 28 $ kN = $ 28 \times 10^3 $ N

⦾ Step 1: Stress Formula
The axial stress $ \sigma $ is given by:
\[ \sigma = \frac{F}{A} \]
⦾ Step 2: Substituting the values
\[ \sigma = \frac{28 \times 10^3}{700} \] \[ \sigma = 40 \text{ MPa} \]
⦾ Final Answer: $ 40 $ MPa (Option A)

📝 A thin cylinder of inner radius 500 mm and thickness 10 mm subjected to an internal pressure of 5MPa. The average circumferential (hoop) stress in MPa is

(A) 100
(B) 250
(C) 500
(D) 1000

Solution =

⦾ Hoop Stress Calculation
A thin cylinder with the following parameters:
✓ Inner radius ($ r $) = 500 mm
✓ Thickness ($ t $) = 10 mm
✓ Internal pressure ($ p $) = 5 MPa

⦾ Solution:
The formula for hoop stress in a thin-walled cylinder is:
\[ \sigma_{\text{hoop}} = \frac{p \cdot r}{t} \] Substitute the given values:
\[ \sigma_{\text{hoop}} = \frac{5 \, \text{MPa} \times 500 \, \text{mm}}{10 \, \text{mm}} \] ⦾ Calculate the result:
\[ \sigma_{\text{hoop}} = \frac{2500}{10} = 250 \, \text{MPa} \] Therefore, the average circumferential (hoop) stress is:
$\boxed{250 \, \text{MPa}}$ (Option b)

📝 A thin walled spherical shell is subjected to an internal pressure. If the radius of the shell is increased by 1% and the thickness is reduced by 1%, with the internal pressure remaining the same, the percentage change in the circumferential (hoop) stress is ____ .

(A) 0
(B) 1
(C) 1.08
(D) 2.02

Solution =

⦾ Hoop Stress Change Calculation: A thin-walled spherical shell subjected to internal pressure undergoes the following changes:
✓ Radius increases by 1% → $ r’ = 1.01r $
✓ Thickness decreases by 1% → $ t’ = 0.99t $
✓ Internal pressure ($ p $) remains the same.

⦾ Solution: The hoop stress formula for a thin-walled spherical shell is:
\[ \sigma = \frac{p \cdot r}{2t} \] Initial stress:
\[ \sigma_{\text{initial}} = \frac{p \cdot r}{2t} \] New stress:
\[ \sigma_{\text{new}} = \frac{p \cdot r’}{2t’} = \frac{p \cdot 1.01r}{2 \times 0.99t} \] \[= \frac{1.01}{0.99} \cdot \sigma_{\text{initial}} \approx 1.0202 \cdot \sigma_{\text{initial}} \] ⦾ Percentage change:
\[ \text{Percentage Change} \] \[= (1.0202 – 1) \times 100 = 2.02\% \] $\boxed{2.02 \, \% \, \text{(Option d)}}$

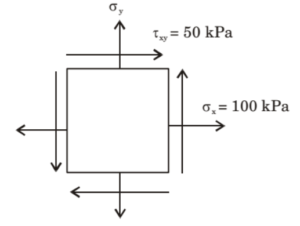
📝 The state of stress at a point, for a body in plane stress, is shown in the figure below. If the minimum principal stress is 10 kPa, then the normal stress σy (in kPa) is ____ .

(A) 9.45
(B) 18.88
(C) 37.78
(D) 75.50

Solution =

⦾ Given:
✓ $ \sigma_x = 100 $ kPa
✓ $ \tau_{xy} = 50 $ kPa
✓ Minimum principal stress $ \sigma_2 = 10 $ kPa

The principal stress formula:
\[ \sigma_{1,2} = \frac{\sigma_x + \sigma_y}{2} \pm \] \[\sqrt{\left(\frac{\sigma_x – \sigma_y}{2}\right)^2 + \tau_{xy}^2} \]
Substituting the values:
\[ 10 = \frac{100 + \sigma_y}{2} – \] \[\sqrt{\left(\frac{100 – \sigma_y}{2}\right)^2 + 50^2} \]
Solving for $ \sigma_y $:
\[ \sqrt{\left(\frac{100 – \sigma_y}{2}\right)^2 + 50^2} \] \[= \frac{100 + \sigma_y}{2} – 10 \]
Squaring both sides and solving, we get:
\[ \sigma_y = 37.78 \text{ kPa} \]
⦾ Answer: (C) 37.78 kPa

📝 A cantilever beam carries the antisymmetric load shown, where Wo is the peak intensity of the distributed load. Qualitatively, the correct bending moment diagram for this beam is ____ .

(A)

(B)

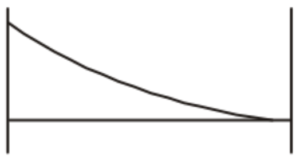
(C)

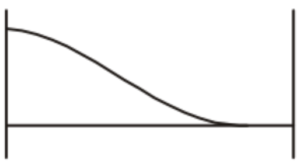
(D)

Solution =

⦾ The correct option is (c) because:

✓ The bending moment is zero at both ends (since it’s a simply supported beam).
✓ The slope of the bending moment diagram is governed by the shear force, which is zero at both ends.
✓ Since the shear force varies non-linearly due to the linearly varying distributed load, the bending moment follows a smooth curved shape.
✓ The moment diagram must be symmetric about the midpoint because the load is antisymmetric.

📝 A solid circular shaft of diameter 100 mm is subjected to an axial stress of 50 MPa. It is further subjected to a torque of 10 kNm. The maximum principal stress experienced on the shaft is closest to

(A) 41 MPa
(B) 82 MPa
(C) 164 MPa
(D) 204 MPa

Solution =

⦾ Step 1: Calculate Shear Stress from Torque
Given:
✓ Diameter (d) = 100 mm ⇒ Radius (r) = 50 mm
✓ Torque (T) = 10 kNm = 10×10⁶ Nmm
Polar moment of inertia:
\[ J = \frac{\pi d^4}{32} = \frac{\pi (100)^4}{32} = \frac{\pi \times 10^8}{32}\, \text{mm}^4 \] Shear stress: \[ \tau = \frac{T \cdot r}{J} = \frac{10 \times 10^6 \times 50}{\frac{\pi \times 10^8}{32}} \] \[= \frac{16000}{\pi} \approx 50.93\, \text{MPa} \]
⦾ Step 2: Calculate Principal Stresses
✓ Given axial stress (σₓ) = 50 MPa
Maximum principal stress: \[ \sigma_1 = \frac{\sigma_x}{2} + \sqrt{\left(\frac{\sigma_x}{2}\right)^2 + \tau^2} \] \[ \sigma_1 = \frac{50}{2} + \sqrt{\left(\frac{50}{2}\right)^2 + (50.93)^2} \] \[ \sigma_1 = 25 + \sqrt{625 + 2593.86} \] \[= 25 + 56.73 = 81.73\, \text{MPa} \]
⦾ Step 3: Compare with Options
Calculated maximum principal stress: 81.73 MPa

⦾ Closest option: b) 82 MPa (closest match)

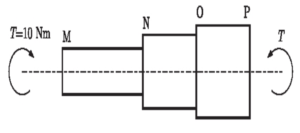
📝 A torque of 1.0 Nm is transmitted through a stepped shaft as shown in figure. The torsional stiffness’s of individual sections of lengths M N, NO and OP are 20 Nm/rad, 30 Nm/rad and 60 Nm/rad respectively. The angular deflection between the ends M and P of the shaft is

(A) 0.5 rad
(B) 1.0 rad
(C) 5.0 rad
(D) 10.0 rad

Solution =

We use the formula for angular deflection:
\[ \theta = \frac{T}{k} \]
⦾ Where:
✓ $ T $ is the applied torque (Nm)
✓ $ k $ is the torsional stiffness (Nm/rad)
✓ $ \theta $ is the angular deflection (rad)

⦾ Given:
✓ $ T = 10 \, \text{Nm} $
✓ $ k_{MN} = 20 \, \text{Nm/rad} $
✓ $ k_{NO} = 30 \, \text{Nm/rad} $
✓ $ k_{OP} = 60 \, \text{Nm/rad} $

⦾ Calculate each segment’s deflection:
\[ \theta_{MN} = \frac{10}{20} = 0.5 \, \text{rad} \] \[ \theta_{NO} = \frac{10}{30} \approx 0.333 \, \text{rad} \] \[ \theta_{OP} = \frac{10}{60} \approx 0.167 \, \text{rad} \]
⦾ Total deflection between M and P:
\[ \theta_{\text{total}} = 0.5 + 0.333 + 0.167 = 1.0 \, \text{rad} \]
⦾ Final Answer:
\[ \boxed{1.0 \, \text{rad}} \]

📝 Consider a simply supported beam of length 50h, with a rectangular cross-section of depth h, and width 2h . The beam carries a vertical point load P at its midpoint. The ratio of the maximum shear stress to the maximum bending stress in the beam is:

(A) 0.01
(B) 0.02
(C) 0.05
(D) 0.10

Solution =

1. Maximum Bending Stress $ \sigma_{\text{max}} $:
\[ \sigma_{\text{max}} = \frac{M_{\text{max}} \cdot c}{I} \]
Where:
✓ $ M_{\text{max}} = \frac{PL}{4} = \frac{P \cdot 50h}{4} = \frac{50Ph}{4} $
✓ $ c = \frac{h}{2} $
✓ $ I = \frac{1}{12} \cdot 2h \cdot h^3 = \frac{h^4}{6} $
\[ \sigma_{\text{max}} = \frac{\left(\frac{50Ph}{4}\right) \cdot \frac{h}{2}}{\frac{h^4}{6}} = \frac{50Ph^2}{8} \cdot \frac{6}{h^4} \] \[= \frac{300P}{8h^2} = \frac{75P}{2h^2} \]
2. Maximum Shear Stress $ \tau_{\text{max}} $:
\[ \tau_{\text{max}} = \frac{3V}{2A} = \frac{3 \cdot \frac{P}{2}}{2 \cdot 2h \cdot h} = \frac{3P}{8h^2} \]
3. Ratio:
\[ \frac{\tau_{\text{max}}}{\sigma_{\text{max}}} = \frac{\frac{3P}{8h^2}}{\frac{75P}{2h^2}} = \frac{3}{8} \cdot \frac{2}{75} = \frac{6}{600} = 0.01 \]
⦾ Correct Answer: (a) 0.01

📝 For the component loaded with a force F as shown in the figure, the axial stress at the corner point P is

(A) $ \frac{F(3L – b)}{4b^3} $
(B) $ \frac{F(3L + b)}{4b^3} $
(C) $ \frac{F(3L – 4b)}{4b^3} $
(D) $ \frac{F(3L – 2b)}{4b^3} $

Solution =

⦾ The bending moment equation is given as:
$$\frac{M}{I} = \frac{\sigma}{y} = \frac{E}{R}$$
Total stress at point $ P $ is due to axial force and bending:
$$\sigma = \sigma_a + \sigma_b$$
1. Bending Stress:
$$\sigma_b = \frac{3F(L – b)}{4b^3}$$
2. Axial Stress:
$$\sigma_a = \frac{F}{4b^2}$$
3. Total Stress:
\[ \sigma = \frac{3F(L – b)}{4b^3} + \frac{F}{4b^2} \] \[ = \frac{3F(L – b)}{4b^3} + \frac{Fb}{4b^3} \] \[ = \frac{3FL – 3Fb + Fb}{4b^3} \] \[ = \frac{F(3L – 2b)}{4b^3} \]
⦾ Final Answer:
$$\boxed{\sigma = \frac{F(3L – 2b)}{4b^3}}$$

📝 A metal bar of length 100 mm is inserted between two rigid supports and its temperature is increased by $ 10^\circ C $. If the coefficient of thermal expansion is $ 12 \times 10^{-6} $ per $ ^\circ C $ and the Young’s modulus is $ 2 \times 10^5 $ MPa, the stress in the bar is

(A) zero
(B) 12 MPa
(C) 24 MPa
(D) 2400 MPa

Solution =

⦾ To determine the thermal stress in the metal bar, we follow these steps:
1. Calculate the thermal expansion if the bar were free to expand:
The change in length is given by:
\[ \Delta L = \alpha \cdot L \cdot \Delta T \] where:
✓ $\alpha = 12 \times 10^{-6} \, \text{per} \, ^\circ C$ (coefficient of thermal expansion),
✓ $L = 100 \, \text{mm}$ (original length),
✓ $\Delta T = 10^\circ C$ (temperature increase).

Substituting the values:
\[ \Delta L = 12 \times 10^{-6} \times 100 \times 10 \] \[= 0.012 \, \text{mm} \] 2. Determine the strain:
Since the bar is constrained, the strain is:
\[ \epsilon = \frac{\Delta L}{L} = \frac{0.012}{100} = 12 \times 10^{-5} \] 3. Calculate the thermal stress:
The stress is related to the strain by Young’s modulus:
\[ \sigma = E \cdot \epsilon \] where $E = 2 \times 10^5 \, \text{MPa}$.
Substituting the values:
\[ \sigma = 2 \times 10^5 \times 12 \times 10^{-5} = 24 \, \text{MPa} \] ⦾ Final Answer: The stress in the bar is $\boxed{24 \, \text{MPa}}$, which corresponds to option (C).

📝 The symmetry of stress tensor at a point in the body under equilibrium is obtained from

(A) Conserved of mass
(B) Force equilibrium equations
(C) Moment equilibrium equations
(D) Conservation of energy

Solution =

⦾ Key Concept:
The symmetry of the stress tensor ($\sigma_{ij} = \sigma_{ji}$) is a fundamental property that comes from the moment equilibrium equations (also called angular momentum equilibrium) at a point in a continuum body.

⦾ Explanation:
✓ Force equilibrium (Option B) gives the balance of linear momentum but doesn’t imply stress tensor symmetry.
✓ Moment equilibrium (Option C) requires that the net moment about any point must be zero, which directly leads to the conclusion that $\sigma_{ij} = \sigma_{ji}$.
✓ Conservation of mass (Option A) and energy (Option D) are unrelated to stress tensor symmetry.

⦾ Mathematical Derivation:
Considering moments about the origin for an infinitesimal element:
\[ \sum M = 0 \implies \sigma_{xy} = \sigma_{yx}, \] \[\quad \sigma_{yz} = \sigma_{zy}, \quad \sigma_{zx} = \sigma_{xz} \] ⦾ Final Answer: The symmetry of the stress tensor is obtained from moment equilibrium equations, which corresponds to option (C).

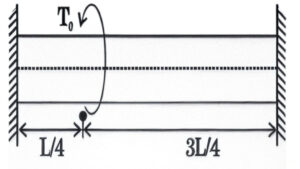
📝 A solid shaft of diameter d and length L is fixed at both the ends. A torque, T0 is applied at a distance, L/4 from the left end as shown in the figure given below.

(A) $ \frac{16T_0}{\pi d^3} $
(B) $ \frac{12T_0}{\pi d^3} $
(C) $ \frac{8T_0}{\pi d^3} $
(D) $ \frac{4T_0}{\pi d^3} $

Solution =

⦾ Given:
✓ Shaft of length $ L $ and diameter $ d $, fixed at both ends
✓ Torque $ T_0 $ applied at $ \frac{L}{4} $ from the left end

⦾ Step 1: Segment the shaft
Let:
✓ Left segment length = $ \frac{L}{4} $
✓ Right segment length = $ \frac{3L}{4} $
✓ Reaction torques: $ T_A $ (left), $ T_B $ (right)

Torque equilibrium:
\[ T_A + T_B = T_0 \tag{1} \]
Equal twist condition (no rotation):
\[ \frac{T_A \cdot \frac{L}{4}}{GJ} = \frac{T_B \cdot \frac{3L}{4}}{GJ} \] \[\Rightarrow T_A = 3T_B \tag{2} \]
Substitute (2) into (1):
\[ 3T_B + T_B = T_0 \Rightarrow 4T_B = T_0 \] \[\Rightarrow T_B = \frac{T_0}{4},\quad T_A = \frac{3T_0}{4} \]
⦾ Step 2: Calculate Maximum Shear Stress
Maximum torque = $ T_A = \frac{3T_0}{4} $
Shear stress in a solid shaft:
\[ \tau = \frac{16T}{\pi d^3} \]
Therefore,
\[ \tau_{\text{max}} = \frac{16 \cdot \frac{3T_0}{4}}{\pi d^3} = \frac{12T_0}{\pi d^3} \]
⦾ Final Answer: (b) $ \frac{12T_0}{\pi d^3} $

📝 A circular rod of length ‘L’ and area of cross-section ‘A’ has a modulus of elasticity ‘E’ and coefficient of thermal expansion ‘α’. One end of the rod is fixed and other end is free. If the temperature of the rod is increased by ∆T, then

(A) Stress developed in the rod is E α ∆T and strain developed in the rod is α ∆T
(B) Both stress and strain developed in the rod are zero.
(C) Stress developed in the rod is zero and strain developed in the rod is α ∆T
(D) Stress developed in the rod is EαΔT and strain developed in the rod is zero

Solution =

⦾ Given Data:
✓ Length of the rod: $ L $
✓ Cross-sectional area: $ A $
✓ Modulus of elasticity: $ E $
✓ Coefficient of thermal expansion: $ \alpha $
✓ Temperature increase: $ \Delta T $
One end is fixed, the other end is free.

⦾ Step 1: Effect of Thermal Expansion
When the temperature increases by $ \Delta T $, the rod expands freely.
The thermal strain is given by:
\[ \varepsilon = \alpha \Delta T \] ⦾ Step 2: Stress Calculation
Stress $ \sigma $ is developed only if there is a restriction preventing expansion. Since one end is free, no stress is induced:
\[ \sigma = 0 \] ⦾ Step 3: Correct Answer
Since the stress is zero and strain is $ \alpha \Delta T $, the correct answer is:
(c) Stress developed in the rod is zero and strain developed in the rod is $ \alpha \Delta T $

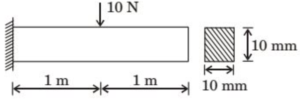
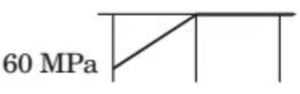
📝 A cantilever beam has the square cross section of 10 mm × 10 mm. It carries a transverse load of 10 N. Considering only the bottom fibres of the beam, the correct representation of the longitudinal variation of the bending stress is

(A)

(B)

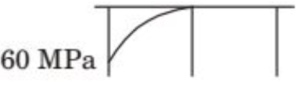
(C)

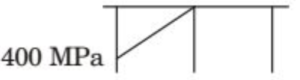
(D)

Solution =

⦾ Step 1: Problem Setup
We have a cantilever beam with a square cross section of $ 10 \, \text{mm} \times 10 \, \text{mm} $, carrying a transverse load of $ 10 \, \text{N} $ at the free end. We need to find the longitudinal variation of bending stress in the bottom fibers of the beam.
✓ Cross section: $ a = 10 \, \text{mm} = 0.01 \, \text{m} $
✓ Load: $ P = 10 \, \text{N} $ (assumed at the free end)
✓ Bottom fibers: These experience tension due to bending.

⦾ Step 2: Bending Stress Formula
The bending stress $ \sigma $ in a beam is given by the flexure formula:
\[ \sigma = \frac{M \cdot c}{I} \] Where:
✓ $ M $: Bending moment at a given section.
✓ $ c $: Distance from the neutral axis to the outermost fiber.
✓ $ I $: Moment of inertia of the cross section.

Moment of Inertia $ I $
For a square cross section of side $ a $:
\[ I = \frac{a^4}{12} = \frac{(0.01)^4}{12} = \frac{0.00000001}{12} = \] \[ 8.333 \times 10^{-9} \, \text{m}^4 \] Distance $ c $
The neutral axis is at the center of the square cross section, so:
\[ c = \frac{a}{2} = \frac{0.01}{2} = 0.005 \, \text{m} \] ⦾ Step 3: Bending Moment Variation
For a cantilever beam with a point load $ P = 10 \, \text{N} $ at the free end ($ x = L $), the bending moment $ M(x) $ at a distance $ x $ from the fixed end ($ x = 0 $) is:
\[ M(x) = P \cdot (L – x) \] At the fixed end ($ x = 0 $): $ M = P \cdot L $
At the free end ($ x = L $): $ M = 0 $
The bending moment varies linearly from a maximum at the fixed end to zero at the free end.

⦾ Step 4: Bending Stress Variation
Since $ \sigma = \frac{M \cdot c}{I} $, and $ c $ and $ I $ are constants, $ \sigma $ is directly proportional to $ M $. Thus, the bending stress $ \sigma(x) $ also varies linearly along the length of the beam:
✓ Maximum stress at the fixed end ($ x = 0 $).
✓ Zero stress at the free end ($ x = L $).

⦾ Step 5: Calculate Maximum Stress
At the fixed end ($ x = 0 $), the maximum bending moment is:
\[ M_{\text{max}} = P \cdot L = 10 \cdot L \] The maximum stress is:
\[ \sigma_{\text{max}} = \frac{M_{\text{max}} \cdot c}{I} = \frac{(10 \cdot L) \cdot (0.005)}{8.333 \times 10^{-9}} \] \[ \sigma_{\text{max}} = \frac{0.05 \cdot L}{8.333 \times 10^{-9}} \] \[= 6 \times 10^6 \cdot L \, \text{Pa} = 6 \cdot L \, \text{MPa} \] The diagrams show maximum stresses of either $ 60 \, \text{MPa} $ or $ 400 \, \text{MPa} $:
If $ \sigma_{\text{max}} = 60 \, \text{MPa} $, then $ 6 \cdot L = 60 $, so $ L = 10 \, \text{m} $.
If $ \sigma_{\text{max}} = 400 \, \text{MPa} $, then $ 6 \cdot L = 400 $, so $ L = 66.67 \, \text{m} $.
A length of $ 10 \, \text{m} $ is more reasonable for a beam with a $ 10 \, \text{mm} \times 10 \, \text{mm} $ cross section, so we assume the maximum stress is $ 60 \, \text{MPa} $.

⦾ Step 6: Match the Diagram
The stress varies linearly from $ 60 \, \text{MPa} $ at the fixed end to $ 0 $ at the free end. Comparing with the diagrams:
✓ A: Linear variation, $ 60 \, \text{MPa} $ at the fixed end, decreasing to 0.
✓ B: Curved variation, $ 60 \, \text{MPa} $, not linear.
✓ C: Linear variation, but $ 400 \, \text{MPa} $.
✓ D: Curved variation, $ 400 \, \text{MPa} $.

⦾ Final Answer
The correct representation of the longitudinal variation of the bending stress in the bottom fibers of the beam is Diagram A.

📝 A simply supported beam of length L is subjected to a varying distributed load \[ w(x) = \sin\left(\frac{3\pi x}{L}\right) \ \text{N/m} \] where $ x $ is the distance measured from the left support. The magnitude of the vertical reaction force in N at the left support is

(A) Zero
(B) $ \frac{L}{3\pi} $
(C) $ \frac{L}{\pi} $
(D) $ \frac{2L}{3\pi} $

Solution =

⦾ Given:
✓ Beam length: $ L $
✓ Distributed load: $ w(x) = \sin\left(\frac{3\pi x}{L}\right) $ N/m
✓ Simply supported at both ends
Find the magnitude of the vertical reaction force at the left support ($ R_A $).

1. Calculate Total Load:
Integrate the distributed load over the beam length:
\[ W = \int_0^L \sin\left(\frac{3\pi x}{L}\right) \, dx \] \[= \left[ -\frac{L}{3\pi} \cos\left(\frac{3\pi x}{L}\right) \right]_0^L \] \[ W = -\frac{L}{3\pi} \left[ \cos(3\pi) – \cos(0) \right] \] \[= -\frac{L}{3\pi} (-2) = \frac{2L}{3\pi} \] 2. Moment Equilibrium about Left Support:
To find $ R_B $, take moments about point A:
\[ \sum M_A = 0 \implies R_B \cdot L \] \[= \int_0^L x \cdot \sin\left(\frac{3\pi x}{L}\right) \, dx \] Solving the integral (using integration by parts):
\[ \int x \sin\left(\frac{3\pi x}{L}\right) \, dx = \frac{L^2}{3\pi} \] \[ R_B = \frac{L}{3\pi} \] 3. Vertical Force Equilibrium:
\[ R_A + R_B = \frac{2L}{3\pi} \] \[\implies R_A = \frac{2L}{3\pi} – \frac{L}{3\pi} = \frac{L}{3\pi} \] 4. Consider Antisymmetric Nature:
The load distribution is antisymmetric about the midpoint, resulting in equal magnitude but opposite direction reactions.

Thus the magnitude is:
\[ |R_A| = \frac{L}{3\pi} \] ⦾ Final Answer: The magnitude of the vertical reaction force at the left support is:
\[ \boxed{\frac{L}{3\pi}} \] Which corresponds to option b) in the given choices.

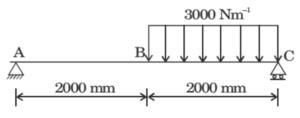
📝 A massless beam has a loading pattern as shown in the figure. The beam is of rectangular cross-section with a width of 30 mm and height of 100 mm. The maximum magnitude of bending stress (in MPa) is given by___.

(A) 60.0
(B) 67.5
(C) 200.0
(D) 225.0

Solution =

⦾ Given:
✓ Uniformly Distributed Load (UDL): $ w = 3000 \, \text{N/m} $
✓ Length of beam: $ 2000 + 2000 = 4000 \, \text{mm} = 4 \, \text{m} $
✓ Width of cross-section: $ b = 30 \, \text{mm} $
✓ Height of cross-section: $ h = 100 \, \text{mm} $

⦾ Step 1: Reaction forces
\[ R_A + R_B = 3000 \times 2 = 6000 \, \text{N} \] Taking moment about A: \[ 6000 \times 3 – R_B \times 4 = 0 \Rightarrow R_B = 4500 \, \text{N} \] \[ \therefore R_A = 1500 \, \text{N} \] ⦾ Step 2: Shear Force and Zero SF Point
\[ \text{Zero SF at } x \text{ from B:} \quad \] \[-4500 + 3000x = 0 \Rightarrow x = 1.5 \, \text{m} \] Hence, the point of maximum bending moment is 1.5 m from point B.

⦾ Step 3: Bending Moment at Maximum Point
\[ BM_{x-x} = -3000 \left( \frac{x^2}{2} \right) + 4500x \] Substituting $ x = 1.5 $: \[ BM_D = -3000 \left( \frac{1.5^2}{2} \right) + 4500 \times 1.5 \] \[= 3375 \, \text{Nm} \] ⦾ Step 4: Section Modulus
\[ Z = \frac{1}{6} b h^2 = \frac{1}{6} \times 30 \times 100^2 \] \[= 50000 \, \text{mm}^3 \] ⦾ Step 5: Maximum Bending Stress
\[ \sigma_{\text{max}} = \frac{M_{\text{max}}}{Z} = \frac{3375 \times 10^3}{50000} \] \[= 67.5 \, \text{MPa} \] ⦾ Final Answer: $ \boxed{67.5 \, \text{MPa}} $

📝 A cantilever beam having square cross-section of side a is subjected to an end load, If a is increased by 19%, the tip deflection decreases approximately by

(A) 19%
(B) 29%
(C) 41%
(D) 50%

Solution =

The deflection at the free end of a cantilever beam under a point load is given by:
\[ \delta = \frac{PL^3}{3EI} \]
⦾ Where:
✓ $ P $: Load
✓ $ L $: Length of the beam
✓ $ E $: Modulus of Elasticity
✓ $ I $: Moment of inertia

For a square cross-section of side $ a $:
\[ I = \frac{a^4}{12} \quad \Rightarrow \quad \delta \propto \frac{1}{a^4} \]
Now, if $ a $ is increased by 19%, the new side becomes:
\[ a’ = 1.19a \]
New deflection becomes:
\[ \delta’ \propto \frac{1}{(1.19)^4 a^4} \]
\[ \frac{\delta’}{\delta} = \left( \frac{1}{1.19^4} \right) \approx \frac{1}{2.00} = 0.5 \]
Thus, the percentage decrease in deflection is:
\[ (1 – 0.5) \times 100\% = \boxed{50\%} \]
⦾ Final Answer: d) 50%

📝 A torque T is applied at the free end of a stepped rod of circular cross-sections as shown in the figure. The shear modulus of the material of the rod is G. The expression for d to produce an angular twist θ at the free end is ____ .

(A) $ \left( \frac{32 T L}{\pi G \theta} \right)^{\frac{1}{4}} $
(B) $ \left( \frac{18 T L}{\pi G \theta} \right)^{\frac{1}{4}} $
(C) $ \left( \frac{16 T L}{\pi G \theta} \right)^{\frac{1}{4}} $
(D) $ \left( \frac{2 T L}{\pi G \theta} \right)^{\frac{1}{4}} $

Solution =

⦾ Given:
✓ Torque $ T $ applied at the free end
✓ Two segments: Length $ L $, diameter $ 2d $
✓ Length $ \frac{L}{2} $, diameter $ d $
✓ Shear modulus = $ G $
✓ Total angle of twist at free end = $ \theta $

⦾ Step 1: Formula for angle of twist
\[ \theta = \frac{T L}{G J} \]
⦾ Step 2: Polar moment of inertia for circular shaft
\[ J = \frac{\pi d^4}{32} \]
⦾ Step 3: Compute twist in each section
✓ Segment 1 (diameter $ 2d $, length $ L $):
\[ J_1 = \frac{\pi (2d)^4}{32} = \frac{16 \pi d^4}{32} = \frac{\pi d^4}{2} \]
\[ \theta_1 = \frac{T L}{G \cdot \frac{\pi d^4}{2}} = \frac{2 T L}{\pi G d^4} \]
✓ Segment 2 (diameter $ d $, length $ \frac{L}{2} $):
\[ J_2 = \frac{\pi d^4}{32} \]
\[ \theta_2 = \frac{T \cdot \frac{L}{2}}{G \cdot \frac{\pi d^4}{32}} = \frac{16 T L}{\pi G d^4} \]
⦾ Step 4: Total twist
\[ \theta = \theta_1 + \theta_2 = \frac{2 T L}{\pi G d^4} + \frac{16 T L}{\pi G d^4} = \frac{18 T L}{\pi G d^4} \]
⦾ Step 5: Solve for $ d $
\[ \theta = \frac{18 T L}{\pi G d^4} \Rightarrow d^4 = \frac{18 T L}{\pi G \theta} \]
\[ \Rightarrow d = \left( \frac{18 T L}{\pi G \theta} \right)^{\frac{1}{4}} \]
⦾ Final Answer: (b) $ \left( \frac{18 T L}{\pi G \theta} \right)^{\frac{1}{4}} $

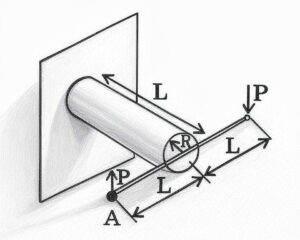
📝 A rigid horizontal rod of length 2L is fixed to a circular cylinder of radius R as shown in the figure. Vertical forces of magnitude P are applied at the two ends as shown in the figure. The shear modulus for the cylinder is G and the Young’s modulus is E. The vertical deflection at point A is____.

(A) $ \frac{PL^3}{\pi R^4 G} $
(B) $ \frac{PL^3}{\pi R^4 E} $
(C) $ \frac{2PL^3}{\pi R^4 E} $
(D) $ \frac{4PL^3}{\pi R^4 G} $

Solution =

We know that: $$ \theta = \frac{TL}{GJ} $$

⦾ Where,
✓ $ T = P(2L) = 2PL $
✓ $ L $ = Length of circular cylinder
✓ $ G $ = Shear Modulus of the cylinder
✓ $ J = \frac{\pi}{32}D^4 = \frac{\pi}{32}(2R)^4 = \frac{\pi}{2}R^4 $

Substituting into the equation for $ \theta $:
$$ \theta = \frac{TL}{GJ} = \frac{2PL \cdot L}{G \cdot \frac{\pi}{2} R^4} = \frac{4PL^2}{\pi G R^4} $$
Deflection at point A:
$$ \Delta_A = \theta \cdot L = \frac{4PL^2}{\pi G R^4} \cdot L = \frac{4PL^3}{\pi G R^4} $$
⦾ Final Answer:
$$ \boxed{ \Delta_A = \frac{4PL^3}{\pi R^4 G} } $$

📝 A seamless pipe of diameter 1 m is to carry fluid under a pressure of 2 N/mm². What should be the minimum thickness of pipe of the maximum stress is not to exceed 80 N/mm² ?

(A) 12.5 mm
(B) 10 mm
(C) 15 mm
(D) 7.5 m

Solution =

⦾ Given:
✓ Diameter of pipe (D) = 1 m = 1000 mm
✓ Internal pressure (P) = 2 N/mm²
✓ Maximum allowable stress (σ) = 80 N/mm²

⦾ Formula:
For a thin-walled pressure vessel (pipe), the circumferential (hoop) stress is given by:
\[ \sigma = \frac{P \cdot D}{2t} \] Where:
t = thickness of the pipe

⦾ Calculation:
Rearranging the formula to solve for thickness (t):
\[ t = \frac{P \cdot D}{2 \cdot \sigma} \] Substituting the given values:
\[ t = \frac{2 \times 1000}{2 \times 80} = \frac{2000}{160} = 12.5 \, \text{mm} \] ⦾ Final Answer: The minimum required thickness of the pipe is $\boxed{12.5 \, \text{mm}}$, which corresponds to option (a).

📝 The ratio of the area under the bending moment diagram to the flexural rigidity between any two points along a beam gives the change in

(A) Deflection
(B) Slope
(C) Shear force
(D) Bending moment

Solution =

⦾ Key Concept:
This problem relates to the moment-area theorems in beam deflection analysis, which connect the bending moment diagram to changes in slope and deflection.

⦾ Relevant Theorem:
The First Moment-Area Theorem states:
\[ \Delta\theta =\]\[ \frac{\text{Area of M/EI dig. between 2 points}}{EI} \] ⦾ where:
✓ Δθ = change in slope between two points
✓ M = bending moment
✓ EI = flexural rigidity

⦾ Analysis of Options:
✓ Deflection (a): Related to the moment of the area under M/EI diagram, not just the area
✓ Slope (b): Directly given by the area under M/EI diagram (correct answer)
✓ Shear force (c): Unrelated to this ratio
✓ Bending moment (d): The diagram already shows bending moment

⦾ Mathematical Explanation:
From beam theory:
\[ \frac{d\theta}{dx} = \frac{M}{EI} \] Integrating between two points:
\[ \Delta\theta = \theta_2 – \theta_1 = \int_{x_1}^{x_2} \frac{M}{EI} dx \]\[= \frac{\text{Area under M diagram}}{EI} \] ⦾ Final Answer: The ratio gives the change in slope, which corresponds to option (b).

📝 Which one of the following types of stress- strain relationship best describes the behavior of brittle materials, such as ceramics and thermosetting plastics, (σ = stress and ε = strain)?

(A)

(B)

(C)

(D)

Solution =

Brittle materials, such as ceramics and thermosetting plastics, exhibit almost no plastic deformation before fracture. They typically fail suddenly after reaching their ultimate strength, with minimal elongation.

⦾ Analysis of Given Graphs:
✓ (a): Represents elastic and perfectly plastic behavior, typical of ductile materials like mild steel. (Incorrect)
✓ (b): Shows elastic behavior followed by a small region of plasticity, which is more typical of materials with some ductility. (Incorrect)
✓ (c): Represents perfectly plastic behavior, which is unrealistic for brittle materials. (Incorrect)
✓ (d): Shows a steep linear relationship between stress and strain, followed by sudden failure with no plastic deformation. This is the correct representation of brittle materials. (Correct)

⦾ Correct Answer: (d)

📝 The homogeneous state of stress for a metal part undergoing plastic deformation is \[ T = \begin{pmatrix} 10 & 5 & 0 \\ 5 & 20 & 0 \\ 0 & 0 & -10 \end{pmatrix} \] Where the stress component values are in MPa. Using Von Mises Yield criterion, the value of estimated shear yield stress, in MPa is

(A) 9.50
(B) 16.07
(C) 28.52
(D) 49.41

Solution =

To solve this problem, we need to use the Von Mises Yield Criterion to estimate the shear yield stress ($\tau_y$) from the given stress tensor. The Von Mises stress ($\sigma_{\text{VM}}$) is calculated from the stress tensor, and the shear yield stress is related to the Von Mises stress.

⦾ Given:
The stress tensor $T$ is: \[ T = \begin{pmatrix} 10 & 5 & 0 \\ 5 & 20 & 0 \\ 0 & 0 & -10 \end{pmatrix} \] where the stress components are in MPa.

⦾ Key Concepts:
✓ Von Mises Stress: The Von Mises stress ($\sigma_{\text{VM}}$) is a scalar value used to predict yielding of materials under complex loading conditions. It is calculated from the stress tensor using the formula: \[ \sigma_{\text{VM}} = \sqrt{\frac{1}{2} (\sigma_{11} – \sigma_{22})^2 }\]\[+\sqrt{ (\sigma_{22} – \sigma_{33})^2 + (\sigma_{33} – \sigma_{11})^2 }\]\[+\sqrt{ 6(\sigma_{12}^2 + \sigma_{23}^2 + \sigma_{31}^2) } \]
✓ Shear Yield Stress: The shear yield stress ($\tau_y$) is related to the Von Mises stress by: \[ \tau_y = \frac{\sigma_{\text{VM}}}{\sqrt{3}} \]
⦾ Step-by-Step Solution:
Step 1: Extract Stress Components
From the stress tensor $T$: \[ \sigma_{11} = 10 \, \text{MPa}, \quad \sigma_{22} = 20 \, \text{MPa}, \]\[\quad \sigma_{33} = -10 \, \text{MPa} \] \[ \sigma_{12} = 5 \, \text{MPa}, \quad \sigma_{23} = 0 \, \text{MPa}, \]\[\quad \sigma_{31} = 0 \, \text{MPa} \]
Step 2: Calculate Von Mises Stress
Using the formula for Von Mises stress: \[ \sigma_{\text{VM}} = \sqrt{\frac{1}{2} (\sigma_{11} – \sigma_{22})^2 }\]\[+ \sqrt{(\sigma_{22} – \sigma_{33})^2 + (\sigma_{33} – \sigma_{11})^2 }\]\[+ \sqrt{6(\sigma_{12}^2 + \sigma_{23}^2 + \sigma_{31}^2) } \] Substitute the stress components: \[ \sigma_{\text{VM}} = \sqrt{\frac{1}{2} (10 – 20)^2} +\] \[\sqrt{ (20 – (-10))^2 + (-10 – 10)^2 }+\] \[\sqrt{ 6(5^2 + 0^2 + 0^2)} \] \[ \sigma_{\text{VM}} = \sqrt{\frac{1}{2} (-10)^2 + (30)^2 }\] \[+ \sqrt{(-20)^2 + 6(25) } \] \[ \sigma_{\text{VM}} = \sqrt{\frac{1}{2} \left[ 100 + 900 + 400 + 150 \right]} \] \[ \sigma_{\text{VM}} = \sqrt{\frac{1}{2} \left[ 1550 \right]} \] \[ \sigma_{\text{VM}} = \sqrt{775} \] \[ \sigma_{\text{VM}} \approx 27.84 \, \text{MPa} \]
Step 3: Calculate Shear Yield Stress
Using the relationship between Von Mises stress and shear yield stress: \[ \tau_y = \frac{\sigma_{\text{VM}}}{\sqrt{3}} \] Substitute the Von Mises stress: \[ \tau_y = \frac{27.84}{\sqrt{3}} \] \[ \tau_y \approx \frac{27.84}{1.732} \] \[ \tau_y \approx 16.07 \, \text{MPa} \]
The estimated shear yield stress is approximately: \[ \tau_y \approx 16.07 \, \text{MPa} \]
⦾ Final Answer: b) 16.07

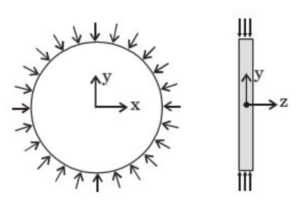
📝 A thin plate of uniform thickness is subject to pressure as shown in the figure below. Under the assumption of plane stress, which one of the following is correct?

(A) Normal stress is zero in the z-direction
(B) Normal stress is tensile in the z-direction
(C) Normal stress is compressive in the z-direction
(D) Normal stress varies in the z-direction

Solution =

The given figure shows a thin plate subjected to uniform pressure on its surface. Under the assumption of plane stress, the normal stress in the thickness direction $ (z\text{-direction}) $ can be analyzed as follows:

⦾ Key Concepts:
✓ Plane Stress Condition: In thin plates, the stress in the thickness direction $ (z) $ is negligible because no significant forces act perpendicular to the plane.
✓ Normal Stress in $ z $-Direction ($ \sigma_z $): In plane stress, we assume that $ \sigma_z = 0 $, meaning there is no normal stress in the thickness direction.
This is valid when the plate is thin and no significant forces act in the $ z $-direction.

⦾ The correct option is: (a) Normal stress is zero in the $ z $-direction.

📝 A cantilever beam OP is connected to another beam PQ with a pin joint as shown in the figure. A load of 10 kN is applied at midpoint of PQ. The magnitude of bending moment (in kN-m) at fixed end O is______.

(A) 2.5
(B) 5
(C) 10
(D) 25

Solution =

⦾ Step 1: Understand the Setup
We have a cantilever beam $ OP $ (fixed at $ O $, length $ 2 \, \text{m} $) connected to beam $ PQ $ (length $ 1 \, \text{m} $) via a pin joint at $ P $. A load of $ 10 \, \text{kN} $ is applied at the midpoint of $ PQ $, which is $ 0.5 \, \text{m} $ from $ P $. We need to find the bending moment at the fixed end $ O $.

⦾ Step 2: Analyze Beam $ PQ $
Beam $ PQ $ is pinned at $ P $ and has a load at its midpoint (point $ C $). Let’s calculate the reaction forces at $ P $ and $ Q $.
✓ Load at $ C $: $ 10 \, \text{kN} $, at $ 0.5 \, \text{m} $ from $ P $.
✓ Length $ PQ $: $ 1 \, \text{m} $.

Let:
✓ $ V_P $: Vertical reaction force at $ P $ (upward).
✓ $ V_Q $: Vertical reaction force at $ Q $ (upward).

Equilibrium of Beam $ PQ $:
Sum of forces in the vertical direction ($ \sum F_y = 0 $):
\[ V_P + V_Q – 10 = 0 \quad \Rightarrow \]\[\quad V_P + V_Q = 10 \quad (1) \] Sum of moments about point $ P $ ($ \sum M_P = 0 $, clockwise positive):
✓ Moment due to the $ 10 \, \text{kN} $ load at $ C $ (distance $ 0.5 \, \text{m} $): $ -10 \times 0.5 = -5 \, \text{kN-m} $.
✓ Moment due to $ V_Q $ at $ Q $ (distance $ 1 \, \text{m} $): $ V_Q \times 1 $.
\[ -10 \times 0.5 + V_Q \times 1 = 0 \] \[ -5 + V_Q = 0 \quad \Rightarrow \quad V_Q = 5 \, \text{kN} \] Substitute $ V_Q = 5 \, \text{kN} $ into equation (1):
\[ V_P + 5 = 10 \quad \Rightarrow \quad V_P = 5 \, \text{kN} \] So, the reaction forces are:
✓ $ V_P = 5 \, \text{kN} $ (upward at $ P $).
✓ $ V_Q = 5 \, \text{kN} $ (upward at $ Q $).

⦾ Step 3: Analyze Beam $ OP $
Beam $ OP $ is a cantilever beam fixed at $ O $. The pin at $ P $ transmits $ V_P = 5 \, \text{kN} $ downward to $ OP $ (since $ V_P $ was upward on $ PQ $).
✓ Length $ OP $: $ 2 \, \text{m} $.
✓ Force at $ P $: $ 5 \, \text{kN} $ downward.
Bending Moment at $ O $:
The bending moment at the fixed end $ O $ is the force at $ P $ times the distance from $ O $ to $ P $:
\[ M_O = V_P \times \text{distance} = 5 \times 2 \]\[= 10 \, \text{kN-m} \] The problem asks for the magnitude, so:
\[ |M_O| = 10 \, \text{kN-m} \] ⦾ Final Answer: The magnitude of the bending moment at the fixed end $ O $ is $ 10 \, \text{kN-m} $. The correct option is c.

📝 A massless beam has a loading pattern as shown in the figure. The beam is of rectangular crosssection with a width of 30 mm and height of 100 mm. The maximum bending moment occurs at___.

(A) Location B
(B) 2675 mm to the right of A
(C) 2500 mm to the right of A
(D) 3225 mm to the right of A

Solution =

⦾ Given:
✓ UDL = $ 3000 \, \text{N/m} $ over span BC of 2 m
✓ Beam span: $ AB = 2 \, \text{m}, \, BC = 2 \, \text{m} \Rightarrow AC = 4 \, \text{m} $
✓ Supports at A and C

⦾ Step 1: Total Load from UDL
$ \text{Total Load} = 3000 \times 2 = 6000 \, \text{N} $

⦾ Step 2: Calculate Support Reactions
\[ \text{Taking moment about A:} \]\[\quad 6000 \times 3 = R_C \times 4 \]\[\Rightarrow R_C = \frac{18000}{4} = 4500 \, \text{N} \] \[ R_A = 6000 – R_C \]\[= 6000 – 4500 = 1500 \, \text{N} \]
⦾ Step 3: Find Point Where Shear Force is Zero
Maximum bending moment occurs where shear force is zero. Let this point be D, located at distance $ x $ from point B.

⦾ Step 4: Use Similar Triangles in Shear Force Diagram
From geometry: \[ \frac{BD}{DC} = \frac{1500}{4500} = \frac{1}{3} \] Let $ DC = 2 – x $, then: \[ \frac{x}{2 – x} = \frac{1}{3} \Rightarrow 3x = 2 – x \]\[\Rightarrow 4x = 2 \Rightarrow x = \frac{1}{2} \, \text{m} \]
⦾ Step 5: Distance from Point A
\[ AD = AB + BD = 2 + 0.5 = \]\[\boxed{2.5 \, \text{m} = 2500 \, \text{mm}} \]
⦾ Final Answer: (c) 2500 mm to the right of A

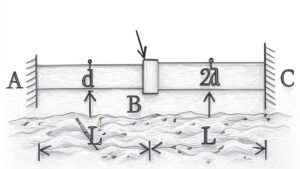
📝 The two shafts AB and BC, of equal length and diameters d and 2d, are made of the same material. They are joined at B through a shaft coupling, while the ends A and C are built-in (cantilevered). A twisting moment T is applied to the coupling. If TA and TC represent the twisting moments at the ends A and C respectively, then

(A) $ T_C = T_A $
(B) $ T_C = 8 T_A $
(C) $ T_C = 16 T_A $
(D) $ T_A = 16 T_C $

Solution =

⦾ Given:
✓ Two shafts AB and BC of equal length $ L $
✓ Diameters: AB = $ d $, BC = $ 2d $
✓ Same material → same shear modulus $ G $
✓ Torque $ T $ applied at point $ B $
✓ Ends A and C are fixed (cantilevered)

From torsion theory, the angle of twist is:
\[ \theta = \frac{T \cdot L}{G \cdot J} \]
For equilibrium (since both ends are fixed):
\[ \frac{T_A \cdot L}{G \cdot J_1} = \frac{T_C \cdot L}{G \cdot J_2} \Rightarrow \frac{T_A}{J_1} = \frac{T_C}{J_2} \]
Polar moment of inertia $ J $ for circular shafts:
\[ J = \frac{\pi d^4}{32} \]
So:
\[ J_1 = \frac{\pi d^4}{32}, \quad J_2 = \frac{\pi (2d)^4}{32} = \frac{\pi \cdot 16d^4}{32} \]\[= 16 J_1 \]
Substitute into equilibrium equation:
\[ \frac{T_A}{J_1} = \frac{T_C}{16 J_1} \Rightarrow T_C = 16 T_A \]
⦾ Final Answer: (c) $ T_C = 16 T_A $

📝 Two circular shafts made of same material, one solid (S) and one hollow (H), have the same length and polar moment of inertia. Both are subjected to same torque. Here, θs is the twist and τs is the maximum shear stress in the solid shaft, whereas θH is the twist and τ H is the maximum shear stress in the hollow shaft. Which one of the following is TRUE?

(A) $\theta_S = \theta_H \text{ and } \tau_S = \tau_H$
(B) $\theta_S > \theta_H \text{ and } \tau_S > \tau_H$
(C) $\theta_S < \theta_H \text{ and } \tau_S < \tau_H$
(D) $\theta_S = \theta_H \text{ and } \tau_S < \tau_H$

Solution =

⦾ Given:
✓ Same material: $ G_S = G_H $ (shear modulus)
✓ Same length: $ L_S = L_H $
✓ Same polar moment of inertia: $ J_S = J_H $
✓ Same applied torque: $ T_S = T_H $

⦾ Twist Angle ($\theta$):
The twist angle is given by:
\[ \theta = \frac{TL}{GJ} \] Since $ T $, $ L $, $ G $, and $ J $ are identical for both shafts:
\[ \theta_S = \theta_H \] ⦾ Maximum Shear Stress ($\tau$):
The maximum shear stress is given by:
\[ \tau = \frac{T \cdot r}{J} \] For the solid shaft:
\[ \tau_S = \frac{T \cdot r_S}{J_S} \] For the hollow shaft:
\[ \tau_H = \frac{T \cdot r_H}{J_H} \] Since $ J_S = J_H $ and $ r_H > r_S $ (hollow shaft has larger outer radius for same $ J $):
\[ \tau_H > \tau_S \] ⦾ Conclusion:
✓ Twist angles are equal: $\theta_S = \theta_H$
✓ Maximum shear stress is greater in the hollow shaft: $\tau_H > \tau_S$

⦾ Correct Answer: d) $\theta_S = \theta_H \text{ and } \tau_S < \tau_H$

📝 A compression spring is made of music wire of 2 mm diameter having a shear strength and shear modulus of 800 MPa and 80 GPa respectively. The mean coil diameter is 20 mm, free length is 40 mm and the number of active coils is 10. If the mean coil diameter is reduced to 10 mm, the stiffness of the spring is approximately

(A) decreased by 8 times
(B) decreased by 2 times
(C) increased by 2 times
(D) increased by 8 times

Solution =

⦾ Given:
✓ Wire diameter, $ d = 2 $ mm
✓ Shear modulus, $ G = 80 $ GPa $ = 80 \times 10^3 $ MPa
✓ Initial mean coil diameter, $ D_1 = 20 $ mm
✓ Reduced mean coil diameter, $ D_2 = 10 $ mm
✓ Number of active coils, $ N = 10 $

⦾ Step 1: Spring Stiffness Formula
The stiffness $ k $ of a helical spring is given by:
\[ k = \frac{G d^4}{8 D^3 N} \] where:
✓ $ G $ is the shear modulus,
✓ $ d $ is the wire diameter,
✓ $ D $ is the mean coil diameter,
✓ $ N $ is the number of active coils.

⦾ Step 2: Calculate Initial Stiffness ($ k_1 $)
For $ D_1 = 20 $ mm:
\[ k_1 = \frac{80 \times 10^3 \times (2)^4}{8 \times (20)^3 \times 10} \] \[ k_1 = \frac{80 \times 10^3 \times 16}{8 \times 8000 \times 10} \] \[ k_1 = \frac{1.28 \times 10^6}{6.4 \times 10^5} = 2 \, \text{N/mm} \] ⦾ Step 3: Calculate Stiffness After Reduction ($ k_2 $)
For $ D_2 = 10 $ mm:
\[ k_2 = \frac{80 \times 10^3 \times (2)^4}{8 \times (10)^3 \times 10} \] \[ k_2 = \frac{80 \times 10^3 \times 16}{8 \times 1000 \times 10} \] \[ k_2 = \frac{1.28 \times 10^6}{8 \times 10^4} = 16 \, \text{N/mm} \] ⦾ Step 4: Determine the Change in Stiffness
The ratio of the new stiffness to the original stiffness is:
\[ \frac{k_2}{k_1} = \frac{16}{2} = 8 \] Thus, the stiffness increases by 8 times when the mean coil diameter is halved.

⦾ Explanation:
✓ Spring stiffness is inversely proportional to the cube of the mean coil diameter ($ k \propto \frac{1}{D^3} $).
✓ Reducing $ D $ from 20 mm to 10 mm (by a factor of 2) increases $ k $ by $ 2^3 = 8 $ times.
✓ This is confirmed by the calculations above.

⦾ The correct option is: d) increased by 8 times

📝 The state of stress at a point in a 2-D loading is such that the Mohr’s circle is a point located at 175 MPa on the positive normal stress axis. The directions of maximum and minimum principal stresses at the point “P ” from the Mohr’s circle are

(A) 0, 90°
(B) 90°, 0
(C) 45°, 135°
(D) all directions

Solution =

To determine the directions of principal stresses when Mohr’s circle degenerates to a point, let’s analyze the situation carefully.

⦾ Given:
Mohr’s circle is a single point at 175 MPa on the normal stress axis.

⦾ Key Observations:
1.) Hydrostatic Stress State:
✓ A point Mohr’s circle indicates equal normal stresses in all directions.
✓ There are no shear stresses ($\tau_{xy} = 0$).
✓ Both principal stresses are equal: $\sigma_1 = \sigma_2 = 175\,\text{MPa}$.
2.) Implications for Principal Directions:
✓ In this special case, all directions are principal directions.
✓ There is no unique maximum or minimum principal stress direction.
✓ Every plane experiences the same normal stress (175 MPa) with zero shear stress.

⦾ Why Other Options Are Incorrect:
✓ Options a) and b): Suggest specific orthogonal directions (0°,90° or 90°,0°), which would only be true if there were distinct principal stresses.
✓ Option c): 45° and 135° would be relevant if shear stresses were present, but here $\tau = 0$ for all orientations.

⦾ Conclusion: When Mohr’s circle is a point, all directions are principal directions.

⦾ The correct option is (d) all directions. \[ \boxed{d} \]

📝 The state of stress at a point in a 2-D loading is such that the Mohr’s circle is a point located at 175 MPa on the positive normal stress axis. The maximum and minimum principal stresses respectively, from Mohr’s circle, are:

(A) +175 MPa, −175 MPa
(B) +175 MPa, +175 MPa
(C) 0, −175 MPa
(D) 0, 0

Solution =

To determine the principal stresses from the given Mohr’s circle information, let’s analyze the situation step-by-step.

⦾ Given:
✓ Mohr’s circle is a point located at 175 MPa on the positive normal stress axis.

Interpretation of Mohr’s Circle as a Point:
When Mohr’s circle degenerates to a single point:
✓ This represents a hydrostatic state of stress (no shear stresses).
✓ All normal stresses are equal in all directions.
✓ There is no shear stress ($\tau = 0$).

Principal Stresses:
In this case:
✓ Both principal stresses are equal to the value where the point is located on the normal stress axis.
✓ $\sigma_1 = \sigma_2 = 175\,\text{MPa}$ (no minimum principal stress different from the maximum).

⦾ Why Other Options Are Incorrect:
✓ Option a) Incorrect because there is no negative principal stress.
✓ Option c) Incorrect because the principal stresses are not zero or negative.
✓ Option d) Incorrect because the stress state is not zero.

⦾ Conclusion:
The maximum and minimum principal stresses are both +175 MPa.
The correct option is (b) +175 MPa, +175 MPa. \[ \boxed{b} \]

(A) (10, 10)MPa
(B) (5,10)MPa
(C) (10, 5)MPa
(D) (5, 5)MPa

Solution =

⦾ Given Data:
✓ Radius of cylinder: $ R = 1 $ m
✓ Wall thickness: $ t = 1 $ mm = $ 0.001 $ m
✓ Water depth: $ h = 2 $ m
✓ Mid-depth height: $ h_m = 1 $ m
✓ Density of water: $ \rho = 1000 $ kg/m³
✓ Acceleration due to gravity: $ g = 10 $ m/s²

⦾ Step 1: Pressure at Mid-Depth
\[ P = \rho g h_m \] Substituting values: \[ P = (1000) (10) (1) = 10,000 \text{ Pa} \]\[= 10 \text{ kPa} \]
⦾ Step 2: Circumferential (Hoop) Stress
The formula for hoop stress is:
\[ \sigma_c = \frac{P R}{t} \] Substituting values: \[ \sigma_c = \frac{(10,000) (1)}{0.001} = 10 \times 10^6 \text{ Pa} \]\[ = 10 \text{ MPa} \]
⦾ Step 3: Axial Stress
The formula for axial stress is:
\[ \sigma_a = \frac{P R}{2t} \] Substituting values: \[ \sigma_a = \frac{(10,000) (1)}{2 \times 0.001} = 5 \times 10^6 \text{ Pa} \]\[= 5 \text{ MPa} \]
⦾ Final Answer:
✓ Axial stress: $ \sigma_a = 5 $ MPa
✓ Circumferential (hoop) stress: $ \sigma_c = 10 $ MPa
\[ \boxed{\sigma_a = 5 \text{ MPa}, \quad \sigma_c = 10 \text{ MPa}} \]

📝 A carpenter glues a pair of cylindrical wooden logs by bonding their end faces at an angle of θ = 30º as shown in the figure. The glue used at the interface fails if Criterion 1: the maximum normal stress exceeds 2.5 MPa. Criterion 2: the maximum shear stress exceeds 1.5 MPa. Assume that the interface fails before the logs fail. When a uniform tensile stress of 4 MPa is applied, the interface

(A) fails only because of criterion 1
(B) fails only because of criterion 2
(C) fails because of both criteria 1 and 2
(D) does not fail

Solution =

⦾ Given:
✓ Applied tensile stress: $ \sigma = 4 $ MPa
✓ Inclination angle: $ \theta = 30^\circ $
✓ Failure criteria:
Criterion 1: Maximum normal stress $ \sigma_n > 2.5 $ MPa
Criterion 2: Maximum shear stress $ \tau > 1.5 $ MPa

⦾ Step 1: Normal Stress on the Inclined Plane
Using the transformation equation:
\[ \sigma_n = \sigma \cos^2\theta \]
✓ Substituting the values:
\[ \sigma_n = 4 \cos^2 30^\circ \]
\[ \sigma_n = 4 \times \left(\frac{\sqrt{3}}{2}\right)^2 \]
\[ \sigma_n = 4 \times \frac{3}{4} = 3 \text{ MPa} \]
✓ Since $ 3 > 2.5 $, the interface fails due to criterion 1.

⦾ Step 2: Shear Stress on the Inclined Plane
Using the transformation equation:
\[ \tau = \sigma \sin\theta \cos\theta \]
✓ Substituting the values:
\[ \tau = 4 \sin 30^\circ \cos 30^\circ \]
\[ \tau = 4 \times \frac{1}{2} \times \frac{\sqrt{3}}{2} \]
\[ \tau = 4 \times \frac{\sqrt{3}}{4} = \sqrt{3} \approx 1.73 \text{ MPa} \]
✓ Since $ 1.73 > 1.5 $, the interface fails due to criterion 2.

⦾ Correct answer is: (C) The interface fails because of both criteria 1 and 2.

📝 A stepped steel shaft shown below is subjected to 10 Nm torque. If the modulus of rigidity is 80 GPa, the strain energy in the shaft in N-mm is ___ .

(A) 4.12
(B) 3.46
(C) 1.73
(D) 0.86

Solution =

The strain energy $ U $ stored in a torsional system is given by:
\[ U = \frac{T^2 L}{2G J} \] ⦾ Given Data:
✓ Torque, $ T = 10 $ Nm = $ 10 \times 10^3 $ N-mm
✓ Modulus of rigidity, $ G = 80 $ GPa = $ 80 \times 10^3 $ N/mm²
✓ Length $ L $ and Polar Moment of Inertia $ J $ for both sections

⦾ Polar Moment of Inertia $ J $ for Each Section:
For a circular shaft:
\[ J = \frac{\pi d^4}{32} \] Larger Section:
✓ Diameter, $ d_1 = 50 $ mm
✓ Length, $ L_1 = 100 $ mm
\[ J_1 = \frac{\pi (50)^4}{32} = 3.07 \times 10^6 \text{ mm}^4 \] ⦾ Smaller Section:
✓ Diameter, $ d_2 = 25 $ mm
✓ Length, $ L_2 = 100 $ mm
\[ J_2 = \frac{\pi (25)^4}{32} = 1.92 \times 10^5 \text{ mm}^4 \] ⦾ Strain Energy for Each Section:
\[ U_1 = \frac{(10 \times 10^3)^2 \times 100}{2 \times (80 \times 10^3) \times (3.07 \times 10^6)} \] \[ U_1 = 0.065 \text{ N-mm} \] \[ U_2 = \frac{(10 \times 10^3)^2 \times 100}{2 \times (80 \times 10^3) \times (1.92 \times 10^5)} \] \[ U_2 = 1.665 \text{ N-mm} \] ⦾ Total Strain Energy:
\[ U = U_1 + U_2 = 0.065 + 1.665 \]\[= 1.73 \text{ N-mm} \] ⦾ The correct option is:
(c) 1.73 N-mm

📝 The value of moment of inertia of the section shown in the figure about the X-axis is

(A) $ \mathbf{8.5050 \times 10^6 \text{ mm}^4} $
(B) $ \mathbf{4.8600 \times 10^6 \text{ mm}^4} $
(C) $ \mathbf{7.7625 \times 10^6 \text{ mm}^4} $
(D) $ \mathbf{8.5725 \times 10^6 \text{ mm}^4} $

Solution =

⦾ Given Data:
✓ Outer rectangle: $ B = 60 \text{ mm}, D = 120 \text{ mm} $
✓ Square cutout: $ a = 30 \text{ mm} $
✓ Distance of centroid of cutout from X-X axis: $ d = 45 \text{ mm} $

⦾ Step 1: Moment of Inertia of Outer Rectangle
\[ I_{xx, \text{outer}} = \frac{B D^3}{12} \] \[ I_{xx, \text{outer}} = \frac{60 \times (120)^3}{12} \] \[ I_{xx, \text{outer}} = 8.64 \times 10^6 \text{ mm}^4 \]
⦾ Step 2: Moment of Inertia of a Single Cutout
\[ I_{xx, \text{cutout}} = \frac{a^4}{12} \] \[ I_{xx, \text{cutout}} = \frac{(30)^4}{12} \] \[ I_{xx, \text{cutout}} = 67,500 \text{ mm}^4 \]
⦾ Step 3: Using Parallel Axis Theorem
\[ A = 30 \times 30 = 900 \text{ mm}^2 \] \[ I_{xx, \text{shifted cutout}} = I_{xx, \text{cutout}} + A d^2 \] \[ I_{xx, \text{shifted cutout}} = 67,500 + (900 \times 45^2) \] \[ I_{xx, \text{shifted cutout}} = 67,500 + 1,822,500 \] \[ I_{xx, \text{shifted cutout}} = 1,890,000 \text{ mm}^4 \]
⦾ Step 4: Final Moment of Inertia
Since there are two cutouts: \[ 2 \times I_{xx, \text{shifted cutout}} = 2 \times 1,890,000 \]\[= 3,780,000 \text{ mm}^4 \]
\[ I_{xx} = I_{xx, \text{outer}} – 2 \times I_{xx, \text{shifted cutout}} \] \[ I_{xx} = 8,640,000 – 3,780,000 \] \[ I_{xx} = 4.860 \times 10^6 \text{ mm}^4 \]
⦾ Final Answer: $ \mathbf{4.860 \times 10^6 \text{ mm}^4} $

📝 A hollow shaft (d0 = 2di where d0 and di are the outer and inner diameters respectively) needs to transmit 20 kW power at 3000 RPM. If the maximum permissible shear stress is 30 MPa, d0 is

(A) 11.29 mm
(B) 22.58 mm
(C) 33.87 mm
(D) 45.16 mm

Solution =

We need to determine the outer diameter $ d_0 $ of the hollow shaft. The given conditions are:

✓ Power $ P = 20 $ kW $ = 20000 $ W
✓ Speed $ N = 3000 $ rpm
✓ Maximum shear stress $ \tau_{\text{max}} = 30 $ MPa $ = 30 \times 10^6 $ Pa
✓ Relation between diameters: $ d_0 = 2d_i $

⦾ Step 1: Calculate the Torque ($ T $)
The power transmitted by the shaft is related to the torque and angular velocity by:
\[ P = T \cdot \omega \] where $ \omega = \frac{2\pi N}{60} $ is the angular velocity in rad/s.
\[ \omega = \frac{2\pi \times 3000}{60} = 314.16 \text{ rad/s} \] \[ T = \frac{P}{\omega} = \frac{20000}{314.16} = 63.66 \text{ Nm} \] ⦾ Step 2: Use Torsion Formula for Hollow Shaft
The maximum shear stress in a hollow shaft is given by:
\[ \tau_{\text{max}} = \frac{T \cdot r_0}{J} \] where:
$ r_0 = \frac{d_0}{2} $ is the outer radius,
$ J = \frac{\pi}{32} (d_0^4 – d_i^4) $ is the polar moment of inertia.
Given $ d_0 = 2d_i $, we can express $ J $ as:
\[ J = \frac{\pi}{32} \left(d_0^4 – \left(\frac{d_0}{2}\right)^4\right) \]\[= \frac{\pi}{32} \left(d_0^4 – \frac{d_0^4}{16}\right) = \frac{\pi}{32} \cdot \frac{15}{16} d_0^4 \]\[= \frac{15\pi}{512} d_0^4 \] Substituting $ \tau_{\text{max}} $, $ T $, and $ J $ into the torsion formula:
\[ 30 \times 10^6 = \frac{63.66 \times \frac{d_0}{2}}{\frac{15\pi}{512} d_0^4} \] ⦾ Simplify the equation:
\[ 30 \times 10^6 = \frac{63.66 \times 512}{2 \times 15\pi d_0^3} \] \[ 30 \times 10^6 = \frac{32593.92}{94.248 d_0^3} \] \[ d_0^3 = \frac{32593.92}{94.248 \times 30 \times 10^6} \] \[ d_0^3 = \frac{32593.92}{2.82744 \times 10^9} = 1.152 \times 10^{-5} \text{ m}^3 \] \[ d_0 = \sqrt[3]{1.152 \times 10^{-5}} = 0.02258 \text{ m} \]\[= 22.58 \text{ mm} \] ⦾ Explanation:
✓ The torque is calculated from the power and rotational speed.
✓ The torsion formula is applied to the hollow shaft geometry.
✓ The polar moment of inertia is simplified using the given diameter relation.
✓ The outer diameter $ d_0 $ is solved for using the permissible shear stress.

⦾ The correct option is: b) 22.58 mm

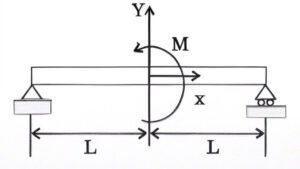
📝 A simply supported beam of length 2L is subjected to a moment M at the mid-point x = 0 as shown in the figure. The deflection in the domain 0 < x < L is given by \[ w = \frac{-Mx}{12EIL}(L – x)(x + c) \] where E is the Young’s modulus, I is the area moment of inertia and C is a constant (to be determined). The slope at the center x = 0 is ___ .

(A) ML/(2EI)
(B) ML/(3EI)
(C) ML/(6EI)
(D) ML/(12EI)

Solution =

⦾ Given: A simply supported beam of length $ 2L $ is subjected to a moment $ M $ at the midpoint $ x = 0 $.
Deflection in the domain $ 0 \leq x \leq L $ is given by:
\[ w = \frac{-Mx}{12EIL}(L – x)(x + c) \]
⦾ Step 1: Expand the Expression
\[ w = \frac{-M}{12EIL} \left[ x(L – x)(x + c) \right] \] \[ = \frac{-M}{12EIL} \left[ x(Lx + Lc – x^2 – cx) \right] \] \[ = \frac{-M}{12EIL} \left[ Lx^2 + Lcx – x^3 – cx^2 \right] \] \[ w = \frac{-M}{12EIL} \left[ (L – c)x^2 + Lc x – x^3 \right] \]
⦾ Step 2: First Derivative (Slope)
\[ \frac{dw}{dx} = \frac{-M}{12EIL} \left[ 2Lx – 3x^2 + Lc – 2cx \right] \]
⦾ Step 3: Second Derivative
\[ \frac{d^2w}{dx^2} = \frac{-M}{12EIL} \left[ 2L – 6x – 2c \right] \] The boundary moment is given by: \[ M = EI \frac{d^2w}{dx^2} \Rightarrow \frac{M}{EI} \]\[= \frac{-M}{12EIL} \left[ 2L – 6x – 2c \right] \]
⦾ Step 4: Apply Boundary Condition at $ x = L $
At $ x = L $, moment = 0: \[ \frac{-M}{12L} \left[ 2L – 6L – 2c \right] = 0 \]\[\Rightarrow -4L – 2c = 0 \Rightarrow c = -2L \]
⦾ Step 5: Final Expression for Slope
Substitute $ c = -2L $ in the first derivative: \[ \frac{dw}{dx} =\]\[ \frac{-M}{12EIL} \left[ 2Lx – 3x^2 – 2Lx + (-2L)L \right] \] At $ x = 0 $: \[ \left. \frac{dw}{dx} \right|_{x = 0} = \frac{-M}{12EIL} (Lc) \]\[= \frac{-M \cdot (-2L^2)}{12EIL} = \frac{ML}{6EI} \]
⦾ Final Answer:
\[ \boxed{\frac{ML}{6EI}} \quad \text{(Option c)} \]
⦾ Points to Remember:
✓ Slope: $ \theta = \frac{dw}{dx} $
✓ Moment: $ M = EI \frac{d^2w}{dx^2} $

📝 The cross-sections of two solid bars made of the same material are shown in the figure. The square cross-section has flexural (bending) rigidity I1 while the circular cross-section has flexural rigidity I2. Both sections have the same cross-sectional area. The ratio I1 /I2 is ?

(A) 1/𝜋
(B) 2/𝜋
(C) 𝜋/3
(D) 𝜋/6

Solution =

⦾ Step 1: Equating areas
✓ Let side of square = $ a $, diameter of circle = $ d $
✓ Area of square: $ a^2 $
✓ Area of circle: $ \frac{\pi d^2}{4} $

Equating areas:
$ a^2 = \frac{\pi d^2}{4} \Rightarrow d^2 = \frac{4a^2}{\pi} \Rightarrow d^4 = \frac{16a^4}{\pi^2} $

⦾ Step 2: Moments of Inertia
✓ Square cross-section: $ I_1 = \frac{a^4}{12} $
✓ Circle cross-section: $ I_2 = \frac{\pi d^4}{64} = \frac{\pi}{64} \cdot \frac{16a^4}{\pi^2} = \frac{a^4}{4\pi} $

⦾ Step 3: Ratio
\[ \frac{I_1}{I_2} = \frac{\frac{a^4}{12}}{\frac{a^4}{4\pi}} = \frac{1}{12} \cdot \frac{4\pi}{1} = \frac{4\pi}{12} = \frac{\pi}{3} \]
⦾ Final Answer: $ \boxed{\frac{\pi}{3}} $

📝 The figure shows the state of stress at a certain point in a stressed body. The magnitudes of normal stresses in the x and y directions are 100 MPa and 20 MPa respectively. The radius of Mohr’s stress circle representing this state of stress is

(A) 120 MPa
(B) 80 MPa
(C) 60 MPa
(D) 40 MPa

Solution =

⦾ Given:
✓ $\sigma_x = 100 \, \text{MPa}$
✓ $\sigma_y = 20 \, \text{MPa}$
✓ $\tau_{xy} = 0$

⦾ Formula for Radius of Mohr’s Circle:
\[ R = \frac{1}{2} \sqrt{(\sigma_x – \sigma_y)^2 + 4\tau_{xy}^2} \]
✓ Substituting values:
\[ R = \frac{1}{2} \sqrt{(100 – 20)^2 + 4(0)^2} \]\[= \frac{1}{2} \sqrt{6400} = \frac{1}{2} \times 80 = 40 \, \text{MPa} \]
⦾ Final Answer: 40 MPa (Option d)

📝 The major and minor principal stresses at a point are 3 MPa and -3 MPa respectively. The maximum shear stress at the point is

(A) zero
(B) 3 MPa
(C) 6 MPa
(D) 9 MPa

Solution =

To determine the maximum shear stress at a point given the principal stresses, we’ll use the relationship between principal stresses and maximum shear stress.

⦾ Given:
✓ Major principal stress ($\sigma_1$) = 3 MPa
✓ Minor principal stress ($\sigma_2$) = -3 MPa

⦾ Formula for Maximum Shear Stress:
The maximum shear stress ($\tau_{\text{max}}$) is given by:
\[ \tau_{\text{max}} = \frac{\sigma_1 – \sigma_2}{2} \] ⦾ Calculation:
Substituting the given principal stresses:
\[ \tau_{\text{max}} = \frac{3\,\text{MPa} – (-3\,\text{MPa})}{2} = \frac{6\,\text{MPa}}{2} \]\[= 3\,\text{MPa} \] ⦾ Conclusion:
The maximum shear stress at the point is 3 MPa.

⦾ The correct option is (B) 3 MPa.

📝 The ratio of the theoretical critical buckling load for a column with fixed ends to that of another column with the same dimensions and material, but with pinned ends, is equal to

(A) 0.5
(B) 1.0
(C) 2.0
(D) 4.0

Solution =

To determine the ratio of the theoretical critical buckling load for a column with fixed ends to that of a column with pinned ends (with the same dimensions and material), we’ll use Euler’s buckling formula and analyze the effective length factors.

⦾ Euler’s Buckling Formula:
The critical buckling load for a column is given by:
\[ P_{cr} = \frac{\pi^2 EI}{(KL)^2} \] ⦾ where:
✓ $ E $ = Modulus of elasticity
✓ $ I $ = Moment of inertia of the cross-section
✓ $ K $ = Effective length factor (depends on end conditions)
✓ $ L $ = Actual length of the column

⦾ Effective Length Factors:
✓ For a column with fixed ends: $ K = 0.5 $
✓ For a column with pinned ends: $ K = 1.0 $

⦾ Buckling Load for Fixed-Ends Column ($ P_{cr,\text{fixed}} $):
\[ P_{cr,\text{fixed}} = \frac{\pi^2 EI}{(0.5L)^2} = \frac{\pi^2 EI}{0.25L^2} \] ⦾ Buckling Load for Pinned-Ends Column ($ P_{cr,\text{pinned}} $):
\[ P_{cr,\text{pinned}} = \frac{\pi^2 EI}{(1.0L)^2} = \frac{\pi^2 EI}{L^2} \] ⦾ Ratio of Buckling Loads:
\[ \frac{P_{cr,\text{fixed}}}{P_{cr,\text{pinned}}} = \frac{\frac{\pi^2 EI}{0.25L^2}}{\frac{\pi^2 EI}{L^2}} = \frac{1}{0.25} = 4 \] ⦾ Conclusion:
The ratio of the critical buckling load for a column with fixed ends to that of a column with pinned ends (same dimensions and material) is 4.0.

⦾ The correct option is (D) 4.0.

📝 A cylindrical container of radius R = 1 m, wall thickness 1 mm is filled with water up to a depth of 2 m and suspended along its upper rim. The density of water is 1000 kg/m³ and acceleration due to gravity is 10 m/s². The self-weight of the cylinder is negligible. The formula for hoop stress in a thin-walled cylinder can be used at all points along the height of the cylindrical container. If the Young’s modulus and Poisson’s ratio of the container material are 100 GPa and 0.3, respectively, the axial strain in the cylinder wall at mid-depth is

(A) $ \mathbf{2 \times 10^{-5}} $
(B) $ \mathbf{6 \times 10^{-5}} $
(C) $ \mathbf{7 \times 10^{-5}} $
(D) $ \mathbf{1.5 \times 10^{-5}} $

Solution =

⦾ Step 1: Given Data
✓ $ E = 100 $ GPa = $ 100 \times 10^9 $ Pa
✓ Poisson’s ratio, $ \nu = 0.3 $
✓ Radius, $ R = 1 $ m
✓ Wall thickness, $ t = 1 $ mm = $ 0.001 $ m
✓ Depth of water = 2 m
✓ Density of water, $ \rho = 1000 $ kg/m³
✓ Gravitational acceleration, $ g = 10 $ m/s²

⦾ Step 2: Pressure at Mid-Depth
Pressure at mid-depth (1 m from the top):
\[ p = \rho g h’ = (1000)(10)(1) = 10^4 \text{ Pa} \] ⦾ Step 3: Hoop and Axial Stress Calculations
Hoop Stress Calculation:
\[ \sigma_c = \frac{p R}{t} = \frac{(10^4)(1)}{10^{-3}} = 10^7 \text{ Pa} \]\[= 10 \text{ MPa} \] ✓ Axial Stress Calculation:
The correct formula for axial stress in a thin-walled cylinder is:
\[ \sigma_a = \frac{\sigma_c}{2} \] Substituting values: \[ \sigma_a = \frac{10^7}{2} = 5 \times 10^6 \text{ Pa} = 5 \text{ MPa} \] ⦾ Step 4: Axial Strain Calculation
The axial strain is given by:
\[ \varepsilon_a = \frac{\sigma_a}{E} – \nu \frac{\sigma_c}{E} \] Substituting values: \[ \varepsilon_a = \frac{5 \times 10^6}{100 \times 10^9} – (0.3) \times \frac{10 \times 10^6}{100 \times 10^9} \] \[ = \frac{5 \times 10^6}{100 \times 10^9} – \frac{3 \times 10^6}{100 \times 10^9} \] \[ = \frac{2 \times 10^6}{100 \times 10^9} \] \[ = 2 \times 10^{-5} \] ⦾ Final Answer:
Axial strain at mid-depth is:
\[ \mathbf{2 \times 10^{-5}} \] Thus, the final result matches option (a).

📝 A bimetallic cylindrical bar of cross sectional area 1 m² is made by bonding Steel (Young’s modulus = 210 GPa) and Aluminium (Young’s modulus = 70 GPa) as shown in the figure. To maintain tensile axial strain of magnitude $ \epsilon = 10^{-6} $ in steel bar and compressive axial strain of magnitude $ \epsilon = 10^{-6} $ in Aluminum bar, the magnitude of the required force P(in kN) along the indicated direction is

(A) 70
(B) 140
(C) 210
(D) 280

Solution =

⦾ Given Data:
✓ Cross-sectional area: $ A = 1 $ m²
✓ Young’s modulus of Steel: $ E_s = 210 $ GPa = $ 210 \times 10^9 $ Pa
✓ Young’s modulus of Aluminum: $ E_a = 70 $ GPa = $ 70 \times 10^9 $ Pa
✓ Tensile strain in Steel: $ \epsilon = 10^{-6} $
✓ Compressive strain in Aluminum: $ \epsilon = 10^{-6} $

⦾ Step 1: Finding the Support Reactions
From Hooke’s Law:
\[ \sigma = E \cdot \epsilon \]
✓ Force in Steel Section:
\[ R_A = A \cdot E_s \cdot \epsilon \]
\[ R_A = (1) \times (210 \times 10^9) \times (10^{-6}) \]
\[ R_A = 210 \times 10^3 = 210 \text{ kN} \]
✓ Force in Aluminum Section:
\[ R_B = A \cdot E_a \cdot \epsilon \]
\[ R_B = (1) \times (70 \times 10^9) \times (10^{-6}) \]
\[ R_B = 70 \times 10^3 = 70 \text{ kN} \]
⦾ Step 2: Finding the Total Force $ P $
\[ P = R_A + R_B \]
\[ P = 210 + 70 \]
\[ P = 280 \text{ kN} \]
⦾ Final Answer:
\[ \boxed{280 \text{ kN} \quad \text{(Option D)}} \]

📝 A solid steel cube constrained on all six faces is heated so that the temperature rises uniformly by ΔT . If the thermal coefficient of the material is α, Young’s modulus is E and the Poisson’s ratio is υ, the thermal stress developed in the cube due to heating is

(A) $-\frac{\alpha(\Delta T)E}{(1-2v)}$
(B) $-\frac{2\alpha(\Delta T)E}{(1-2v)}$
(C) $-\frac{3\alpha(\Delta T)E}{(1-2v)}$
(D) $-\frac{\alpha(\Delta T)E}{3(1-2v)}$

Solution =

⦾ Step 1: Understand the constraints
The cube is constrained in all directions, meaning it cannot expand or contract in any direction: \[ \epsilon_x = \epsilon_y = \epsilon_z = 0 \]
⦾ Step 2: Calculate the thermal strain
If unconstrained, the free thermal strain in each direction would be: \[ \epsilon_{\text{thermal}} = \alpha \Delta T \] But since the cube is constrained, this strain is prevented, resulting in a mechanical strain of: \[ \epsilon_{\text{mechanical}} = -\alpha \Delta T \]
⦾ Step 3: Relate stress and strain
For an isotropic material constrained in all three directions, the stress in each direction ($\sigma$) is: \[ \epsilon_x = \frac{\sigma_x}{E} – \frac{v}{E}(\sigma_y + \sigma_z) \] Due to symmetry ($\sigma_x = \sigma_y = \sigma_z = \sigma$): \[ \epsilon = \frac{\sigma}{E} – \frac{2v\sigma}{E} = \frac{\sigma(1 – 2v)}{E} \] Since the total strain is zero (constrained): \[ \alpha \Delta T + \frac{\sigma(1 – 2v)}{E} = 0 \] Solving for $\sigma$: \[ \sigma = -\frac{\alpha \Delta T E}{(1 – 2v)} \]
The thermal stress developed in the cube is: \[ \sigma = -\frac{\alpha (\Delta T) E}{(1 – 2v)} \]
⦾ The correct option is a): \[ \boxed{-\frac{\alpha(\Delta T)E}{(1-2v)}} \]

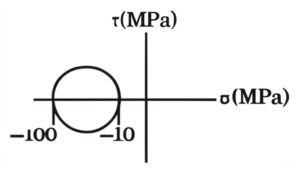
📝 The Mohr’s circle of plane stress for a point in a body is shown. The design is to be done on the basis of the maximum shear stress theory for yielding. Then, yielding will just begin if the designer chooses a ductile material whose yield strength is

(A) 45 MPa
(B) 50 MPa
(C) 90 MPa
(D) 100 MPa

Solution =

⦾ From the Mohr’s Circle diagram:
✓ The center of the circle is at $ \frac{-100 + (-10)}{2} = -55 \, \text{MPa} $
✓ The radius of the circle is $ R = \frac{-10 – (-100)}{2} = 45 \, \text{MPa} $
✓ So, the maximum shear stress is $ \tau_{\text{max}} = 45 \, \text{MPa} $

According to the Maximum Shear Stress Theory (Tresca’s criterion), yielding begins when:
$ \tau_{\text{max}} = \frac{\sigma_y}{2} $

⦾ Substituting the known value:
$ 45 = \frac{\sigma_y}{2} \Rightarrow \sigma_y = 90 \, \text{MPa} $

⦾ Final Answer: 90 MPa

📝 The state of 2D stress at a point is given by a \[ \begin{bmatrix} \sigma_{xx} & \tau_{xy} \\ \tau_{yx} & \sigma_{yy} \end{bmatrix} = \begin{bmatrix} 100 & 30 \\ 30 & 20 \end{bmatrix} \text{MPa} \] The maximum shear stress in MPa is

(A) 50
(B) 75
(C) 100
(D) 110

Solution =

To determine the maximum shear stress at a point given the 2D stress matrix, we’ll follow these steps:

⦾ Given Stress Matrix:
\[ \begin{bmatrix} \sigma_{xx} & \tau_{xy} \\ \tau_{yx} & \sigma_{yy} \end{bmatrix} = \begin{bmatrix} 100 & 30 \\ 30 & 20 \end{bmatrix} \text{MPa} \] ⦾ Step 1: Identify Stress Components
✓ Normal stress in x-direction: $\sigma_{xx} = 100\,\text{MPa}$
✓ Normal stress in y-direction: $\sigma_{yy} = 20\,\text{MPa}$
✓ Shear stress: $\tau_{xy} = \tau_{yx} = 30\,\text{MPa}$

⦾ Step 2: Calculate Principal Stresses
The principal stresses ($\sigma_1, \sigma_2$) are given by:
\[ \sigma_{1,2} = \frac{\sigma_{xx} + \sigma_{yy}}{2} \pm \]\[\sqrt{\left(\frac{\sigma_{xx} – \sigma_{yy}}{2}\right)^2 + \tau_{xy}^2} \] Substituting the values:
\[ \sigma_{1,2} = \frac{100 + 20}{2} \pm \]\[\sqrt{\left(\frac{100 – 20}{2}\right)^2 + 30^2} \] \[ \sigma_{1,2} = 60 \pm \sqrt{40^2 + 30^2} = 60 \pm 50 \] \[ \sigma_1 = 110\,\text{MPa}, \quad \sigma_2 = 10\,\text{MPa} \] ⦾ Step 3: Compute Maximum Shear Stress
The maximum shear stress ($\tau_{\text{max}}$) is half the difference between the principal stresses:
\[ \tau_{\text{max}} = \frac{\sigma_1 – \sigma_2}{2} = \frac{110 – 10}{2} = 50\,\text{MPa} \] ⦾ Conclusion
The maximum shear stress at the point is 50 MPa.

⦾ The correct option is (A) 50.

📝 Two steel column P(length L and yield strength fy = 250 MPa) have the same cross-section and end condition the ratio of bucking load of column P to that of column Q is

(A) 0.5
(B) 1.0
(C) 2.0
(D) 4.0

Solution =

To determine the ratio of the buckling load of column P to that of column Q, let’s analyze the given information and apply Euler’s buckling formula.

⦾ Given:
Both columns P and Q have the same cross-section and same end conditions.
Column P has length L and yield strength f_y = 250 MPa.
Column Q has length 2L (implied from the question, as the ratio is being asked).

⦾ Euler’s Buckling Formula:
The critical buckling load for a column is given by:
\[ P_{cr} = \frac{\pi^2 EI}{(KL)^2} \] ⦾ where:
✓ $ E $ = Modulus of elasticity
✓ $ I $ = Moment of inertia of the cross-section
✓ $ K $ = Effective length factor (depends on end conditions)
✓ $ L $ = Length of the column

⦾ Analysis:
✓ Since both columns have the same cross-section, $ I $ is the same for both.
✓ Both have the same end conditions, so $ K $ is the same for both.
✓ Column P has length $ L $, and column Q has length $ 2L $.

⦾ Buckling Load Ratio:
The buckling load is inversely proportional to the square of the length:
\[ \frac{P_{cr,P}}{P_{cr,Q}} = \frac{(KL_Q)^2}{(KL_P)^2} = \frac{(2L)^2}{L^2} = 4 \] Thus, the ratio of the buckling load of column P to column Q is 4.0.

⦾ Final Answer:
The correct option is (D) 4.0.

📝 The “Plane section remain plane” assumption in bending theory implies

(A) strain profile is linear
(B) stress profile is linear
(C) both profiles are linear
(D) shear deformation is neglected

Solution =

To understand the implication of the “Plane sections remain plane” assumption in bending theory, let’s analyze the statement and the given options:

⦾ Key Assumption in Bending Theory:
The “Plane sections remain plane” assumption states that cross-sections of a beam that are plane before bending remain plane after bending. This leads to the following consequences:
✓ It results in a linear strain distribution across the depth of the beam.
✓ The stress profile is not necessarily linear; it depends on the material behavior (e.g., linear elastic vs. plastic).
✓ Shear deformation is typically neglected in Euler-Bernoulli beam theory, but this is a separate assumption.

⦾ Analysis of Options:
✓ (A) Strain profile is linear: Correct. The assumption directly implies a linear strain distribution.
✓ (B) Stress profile is linear: Incorrect. The stress profile is linear only if the material is linear elastic (Hooke’s law applies).
✓ (C) Both profiles are linear: Incorrect. The stress profile’s linearity depends on material behavior, not just geometry.
✓ (D) Shear deformation is neglected: Incorrect. While shear deformation is often neglected in classical beam theory, this is not the primary implication of the “plane sections remain plane” assumption.

⦾ Conclusion:
The “Plane sections remain plane” assumption primarily implies that the strain profile is linear across the beam’s cross-section.

⦾ The correct option is (A) strain profile is linear.

📝 Creep strain is

(A) caused due to dead load only
(B) caused due to live load only
(C) caused due to cyclic load only
(D) independent of load

Solution =

To determine the correct statement about creep strain, let’s analyze the phenomenon and the given options:

⦾ Definition of Creep Strain:
Creep strain refers to the time-dependent deformation that occurs in materials under a sustained constant load (typically below the yield strength) at elevated temperatures. The key characteristics are:
✓ It occurs under static loads (dead loads)
✓ It is time-dependent
✓ It is more significant at high temperatures

⦾ Analysis of Options:
✓ A) Caused due to dead load only: Correct. Creep occurs under sustained static loads (dead loads), not live or cyclic loads.
✓ B) Caused due to live load only: Incorrect. Live loads are transient and do not cause time-dependent creep.
✓ C) Caused due to cyclic load only: Incorrect. Cyclic loads cause fatigue, not creep.
✓ D) Independent of load: Incorrect. Creep is directly dependent on the applied constant load.

⦾ Conclusion:
Creep strain is primarily caused by dead loads (sustained static loads).

⦾ Final Answer:
The correct option is (A) caused due to dead load only.

📝 A material that has identical properties in all directions is said to be

(A) homogenous
(B) isotropic
(C) elastic
(D) orthotropic

Solution =

To determine the correct term for a material that has identical properties in all directions, let’s analyze the definitions of the given options:

⦾ Definitions:
✓ Homogeneous: A material is homogeneous if its composition and properties are uniform throughout its volume. This does not necessarily imply identical properties in all directions.
✓ Isotropic: A material is isotropic if its mechanical and thermal properties are identical in all directions. This is the correct term for the given description.
✓ Elastic: A material is elastic if it returns to its original shape after the removal of stress. This is unrelated to directional properties.
✓ Orthotropic: A material is orthotropic if its properties vary along three mutually perpendicular axes. This is the opposite of isotropic.

⦾ Conclusion:
A material with identical properties in all directions is termed isotropic.

⦾ The correct option is b) isotropic.

📝 A thin cylindrical pressure vessel with closed-ends is subjected to internal pressure. The ratio of circumferential (hoop) stress to the longitudinal stress is

(A) 0.25
(B) 0.50
(C) 1.0
(D) 2.0

Solution =

To determine the ratio of circumferential (hoop) stress to longitudinal stress in a thin cylindrical pressure vessel with closed ends, let’s analyze the stresses step-by-step.

⦾ Given:
✓ A thin cylindrical pressure vessel with closed ends subjected to internal pressure $ p $.
✓ Inner radius $ r $.
✓ Wall thickness $ t $.

⦾ Circumferential (Hoop) Stress ($ \sigma_h $):
The hoop stress is caused by the internal pressure acting radially outward and is resisted by the tension in the cylindrical wall. The formula for hoop stress is:
\[ \sigma_h = \frac{p \cdot r}{t} \] ⦾ Longitudinal Stress ($ \sigma_l $):
The longitudinal stress arises from the internal pressure acting on the closed ends of the cylinder. The formula for longitudinal stress is:
\[ \sigma_l = \frac{p \cdot r}{2t} \] ⦾ Ratio of Hoop Stress to Longitudinal Stress:
\[ \text{Ratio} = \frac{\sigma_h}{\sigma_l} = \frac{\frac{p \cdot r}{t}}{\frac{p \cdot r}{2t}} = 2 \] ⦾ Final Answer: The ratio of circumferential (hoop) stress to longitudinal stress is 2.0.

(Privacy Policy , Cookie Policy)